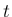 分後の体積
分後の体積 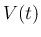 、表面積
、表面積 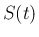 に
対して、「体積減少率 (= 1 分当たりの体積減少) は表面積に比例する」を
に
対して、「体積減少率 (= 1 分当たりの体積減少) は表面積に比例する」を
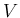 ,
, 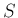 で表しなさい (比例定数は
で表しなさい (比例定数は 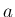 (
(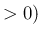 とする)。
とする)。
まず、元の問題は以下の通り。
太陽の下に置いた雪玉の分後の体積
、表面積
に 対して、「体積減少率 (= 1 分当たりの体積減少) は表面積に比例する」を
,
で表しなさい (比例定数は
(
とする)。
これは、時間に対する体積増加率が 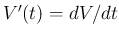 なので、
体積減少率は
なので、
体積減少率は 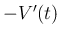 、よって「
、よって「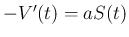 」が正解となるが、
以下のような間違いがかなりあった (しかもそれが間違いであることに
気がついていないようで丸としてある)。
」が正解となるが、
以下のような間違いがかなりあった (しかもそれが間違いであることに
気がついていないようで丸としてある)。
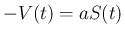 」
」
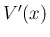 なので」
なので」
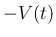 は体積減少率ではなくて、体積の
は体積減少率ではなくて、体積の 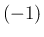 倍。
導関数の意味が理解できていないものと思われる。
倍。
導関数の意味が理解できていないものと思われる。
増加率の変数が 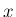 になっているのは、通常の微分が
になっているのは、通常の微分が 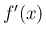 で
あるからの癖か、あるいは私の手書きの正答例の
で
あるからの癖か、あるいは私の手書きの正答例の 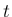 を
を 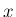 と
見たのかもしれない。
と
見たのかもしれない。
いずれにせよ、導関数の意味に関する問題は、 工学ではむしろ導関数の計算よりも重要かもしれないので、 こういう見方はちゃんとできてもらいたい。 例えば、以下のような日本語と式の対応も正しく把握できる必要がある。
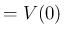
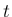 分後までの体積の減少」
分後までの体積の減少」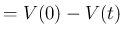
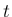 分後までの体積の平均減少率」
分後までの体積の平均減少率」
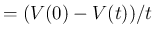
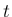 分後時点の体積減少率」
分後時点の体積減少率」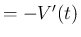
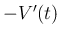 は、丁度
は、丁度 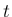 分後の時点での減少率であって、
極限によって定義される「微分係数」(導関数の値) を意味し、
「平均減少率」は極限を取らない平均的な変化率を意味する。
分後の時点での減少率であって、
極限によって定義される「微分係数」(導関数の値) を意味し、
「平均減少率」は極限を取らない平均的な変化率を意味する。
数学の教科書では、よく
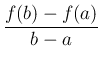 を平均変化率、
を平均変化率、
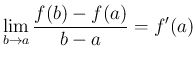 を微分係数と呼んでいるが、
それに対応する。「2 点の傾き」と「その点での接線の傾き」、
あるいは「平均速度」と「瞬間的な速度」も同様の関係にある。
を微分係数と呼んでいるが、
それに対応する。「2 点の傾き」と「その点での接線の傾き」、
あるいは「平均速度」と「瞬間的な速度」も同様の関係にある。
竹野茂治@新潟工科大学