5 半径 1 の球の体積の計算
この節では、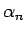 (
(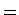 半径 1 の球の体積) を計算する。
これまで、
半径 1 の球の体積) を計算する。
これまで、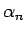 は
は 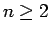 で考えていたが、
(8) が
で考えていたが、
(8) が 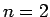 ,
, 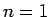 でも成り立つように、
でも成り立つように、
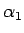 ,
, 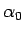 を
を
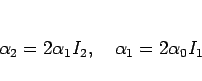
を満たすように決めることにすると、
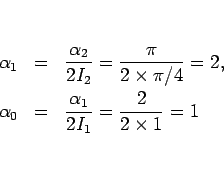
となり、このようにすれば (8) は 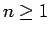 に対して成り立つことになる。
に対して成り立つことになる。
よって、(8) から 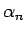 を帰納的に求めてみると、
を帰納的に求めてみると、
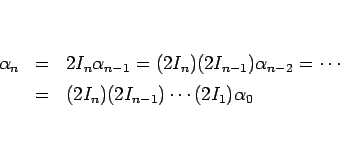
となるので、結局
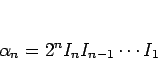 |
(11) |
と書けることになる。
ここで (10) より容易に、
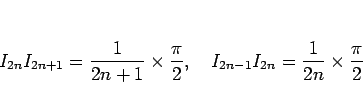
であることがわかり、よっていずれにしても
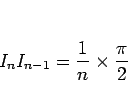 |
(12) |
が成り立つ。
これにより、(11) の右辺を 2 つずつまとめて考えればよいので、
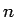 が偶数の場合と奇数の場合に分けて考えると、以下のようになる。
が偶数の場合と奇数の場合に分けて考えると、以下のようになる。
そしてこの 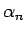 に対し、
に対し、
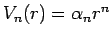 となることになる。
となることになる。
竹野茂治@新潟工科大学
2007年8月6日
![]() を帰納的に求めてみると、
を帰納的に求めてみると、