4 1 以下の勾配への帰着
次に、1 以下の 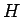 に帰着させることを考える。
そのためには、公式
に帰着させることを考える。
そのためには、公式
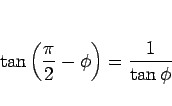 |
(4) |
や、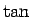 の加法定理
の加法定理
 |
(5) |
を用いる。公式 (4) は
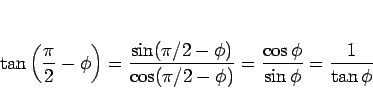
より得られるし、また 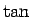 の加法定理は、
の加法定理は、
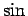 ,
, 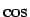 の加法定理から以下のようにして容易に得られる。
の加法定理から以下のようにして容易に得られる。
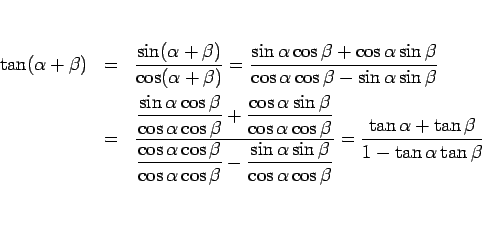
(4) より、
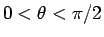 に対して (
に対して (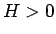 )
)
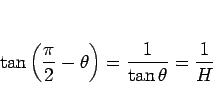
であるから、
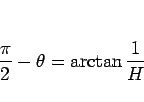 |
(6) |
と求められることになる。
すなわち、
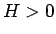 のときは (3) と (6) の
どちらを用いても
のときは (3) と (6) の
どちらを用いても 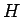 から
から 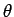 を求めることができるので、
を求めることができるので、
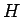 と
と 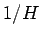 の小さい方を使って求めればよいことになる。
の小さい方を使って求めればよいことになる。
よって、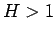 ならば、
ならば、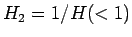 に対して
に対して
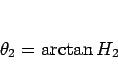
とすれば、
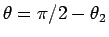 として求められるし、
として求められるし、
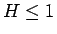 ならそのまま (3) で求めることにすれば、
これで、
ならそのまま (3) で求めることにすれば、
これで、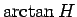 の計算はどちらにしても
の計算はどちらにしても 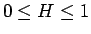 の場合に帰着されることになる。
そしてこの場合は
の場合に帰着されることになる。
そしてこの場合は 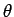 は
は
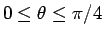 となる。
となる。
竹野茂治@新潟工科大学
2009年1月18日
![]() に対して (
に対して (![]() )
)
![]() ならば、
ならば、![]() に対して
に対して