2 アークタンジェントの展開式
まず、アークタンジェントのマクローリン展開式を紹介する。
なお、タンジェントの逆関数であるアークタンジェントは、
 や
や 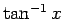 と書かれることもあるが、
本稿では統一して
と書かれることもあるが、
本稿では統一して  と書くことにする。
と書くことにする。
またマクローリン展開式も、
定義通りの微分による計算では規則性を見出すのが難しいので、
ここでは別な方法で求めることにする。
無限等比数列の和の公式
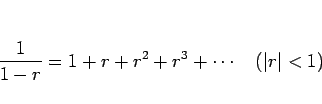
で 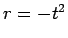 (
(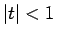 ) とすると
) とすると
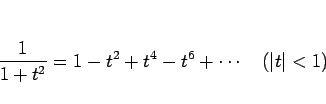
が成り立つ。これを、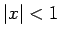 である
である 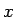 に対し
に対し 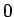 から
から 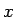 まで積分すると、
まで積分すると、
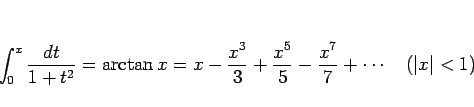 |
(1) |
となる。これが  のマクローリン展開である。
のマクローリン展開である。
竹野茂治@新潟工科大学
2009年1月18日