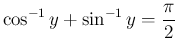 (
(
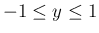 )
)
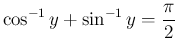 (
(
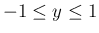 )
)
に対し
,
と すると、
,
,
,
なので、
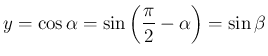
となり、証明からもわかるが、これは、ほぼより
だから
となる。 よって
(証明おわり)
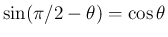 という
性質を逆三角関数の言葉で表したものである。
という
性質を逆三角関数の言葉で表したものである。
また、これはグラフからも容易にわかる。
それは、
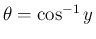 のグラフは、
のグラフは、
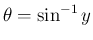 のグラフを上下反転させて、
のグラフを上下反転させて、
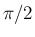 だけ上にあげたグラフとなっているからである。
だけ上にあげたグラフとなっているからである。
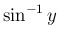 ,
, 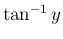 は奇関数
は奇関数
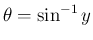 ,
,
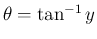 のグラフが
原点対称になっていることからわかる。
だから、負の
のグラフが
原点対称になっていることからわかる。
だから、負の 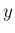 に対するこれらの値は、例えば
に対するこれらの値は、例えば
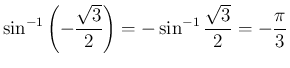
一方、
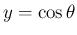 は偶関数、
すなわち
は偶関数、
すなわち 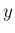 軸に関してグラフが対称だが、
軸に関してグラフが対称だが、
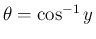 は偶関数でも奇関数でもない。
は偶関数でも奇関数でもない。
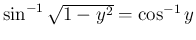 (
(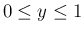 )
)
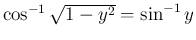 (
(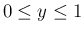 )
)
に対し
とすると、
より
で、
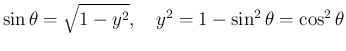
となり、これは、証明からもわかるが、ほぼ,
より
となるから、
より
となる。 後者も同様。(証明おわり)
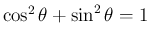 を
逆三角関数の言葉で表したものである。
を
逆三角関数の言葉で表したものである。
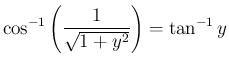 (
(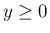 )
)
に対し
とすると、
,
となる。よって、
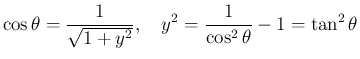
となり、これは、,
より
, よって
となる。
(証明おわり)
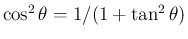 を逆三角関数で表現したもの。
を逆三角関数で表現したもの。
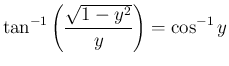 (
(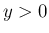 )
)
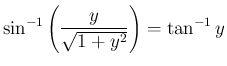
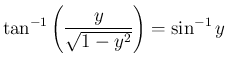
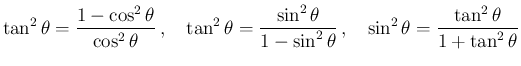
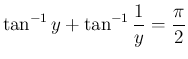 (
(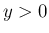 )
)
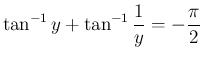 (
(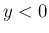 )
)
に対し
とすると、
,
となる。 ここで、
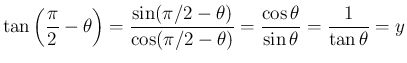
となるので、より
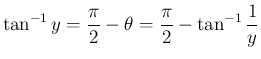
となる。
一方、に対し
とすると、
なので、
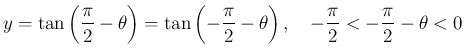
となり、よって
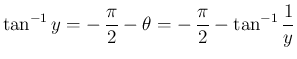
となる。(証明おわり)これらも、ほぼ
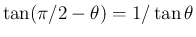 を逆三角関数に
読み替えたもの。
を逆三角関数に
読み替えたもの。
次は加法定理から得られるものを紹介する。
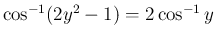 (
( )
)
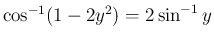 (
(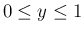 )
)
に対し
とすると
,
で、
となるが、
,
なので、
となる。
後者も同様。(証明おわり)これらは、倍角の公式
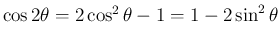 を
逆三角関数に読み替えたもの。
を
逆三角関数に読み替えたもの。
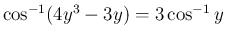 (
(
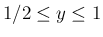 )
)
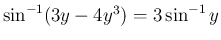 (
(
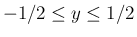 )
)
まずが
では
から
に 単調増加することに注意する (
から容易にわかる)。 よって、
とすると
で、
となる。 このとき、
となり、
,
なので、
となる。
後者も、これは、三倍角の公式が
では
から 1 に 単調増加することからほぼ同様に示される。 (証明おわり)
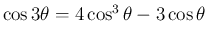 ,
,
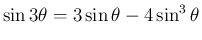 を逆三角関数に読み替えたもの。
を逆三角関数に読み替えたもの。
ちなみに、
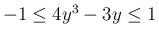 は
は
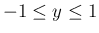 で成り立つが、
角の範囲が変わるので、例えば前者は、
で成り立つが、
角の範囲が変わるので、例えば前者は、
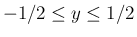 の場合は、
の場合は、
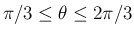 より
より
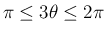 と
なってしまうので、
と
なってしまうので、
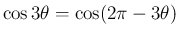 から、
また
から、
また
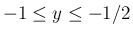 の場合は、
の場合は、
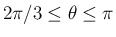 より
より
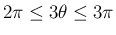 と
なってしまうので、
と
なってしまうので、
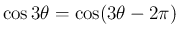 から、
から、
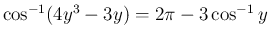 (
(
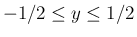 )
)
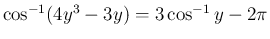 (
(
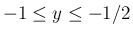 )
)
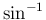 の方も同様である。
の方も同様である。
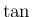 は加法定理が
は加法定理が 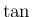 だけで表されるので、
倍角の公式でなくても加法定理から直接次の公式が得られる。
だけで表されるので、
倍角の公式でなくても加法定理から直接次の公式が得られる。
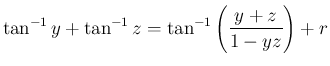
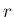 は
は 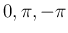 のいずれかで、
のいずれかで、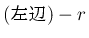 が
が
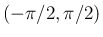 に
入るように選ぶ。
に
入るように選ぶ。
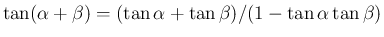 から容易に得られる。
から容易に得られる。
竹野茂治@新潟工科大学