2 循環論法
まず、(1) にまつわる循環論法について説明しておく。
元々「円周率 (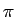 )」は、円の面積から定義するものではなく、
円の円周と直径の比として定義される:
)」は、円の面積から定義するものではなく、
円の円周と直径の比として定義される:
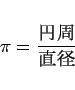 |
(2) |
よって、
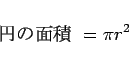 |
(3) |
であるという事実は円周率の定義ではなく、
(2) から導かなければいけない「定理」である。
現代数学では、円のように、
 |
(4) |
と考えられているので、その立場からすれば、
半径 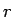 の円の面積
の円の面積 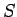 は定積分
は定積分
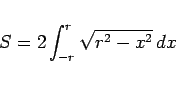 |
(5) |
によって定義されることになる。
この積分の計算には、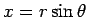
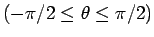 の
ような置換積分が用いられ、
の
ような置換積分が用いられ、
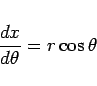 |
(6) |
より、
となる。
さて、(1) の証明であるが、
まず、
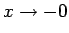 に対しては、
に対しては、
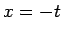 とすれば
とすれば
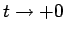 となり、
となり、
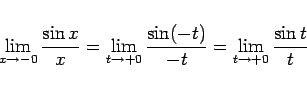 |
(8) |
となるので、
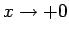 の方だけを考えればよい。
の方だけを考えればよい。
そして、その極限が 1 にあることを示すには「はさみうちの原理」を
使うのであるが、扇形の面積を使う方法は以下の通り (図 1)。
中心角 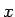 (ラジアン)、半径 1 の扇形で、
(ラジアン)、半径 1 の扇形で、
 |
(9) |
という面積に関する不等式を考えれば、
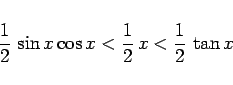 |
(10) |
なので、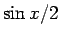 で割れば、
で割れば、
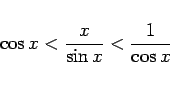
となり、
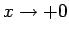 とすれば、はさみうちの原理によって
とすれば、はさみうちの原理によって
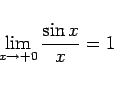 |
(11) |
が得られる、という論法である。
 OAC の代わりに
OAC の代わりに  OBC (=
OBC (=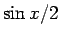 ) を使うこともあるが、
違いはほとんどない。
) を使うこともあるが、
違いはほとんどない。
そして、(1) を元にして、
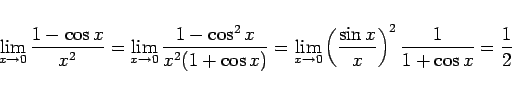 |
(12) |
が得られ、(1) と (12) により、
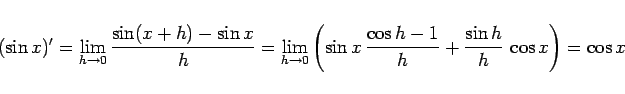 |
(13) |
と 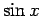 の導関数が得られる。
の導関数が得られる。
さて、ここまでの話でどこが循環論法かと言えば、
それは (9) で使用した扇形の面積である。
扇形 OBC の面積が 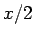 になる、ということには、
円の面積の公式 (3) を使っていることになるが、
円の面積は (5) によって定義され、
それは (7) で見たように
になる、ということには、
円の面積の公式 (3) を使っていることになるが、
円の面積は (5) によって定義され、
それは (7) で見たように 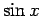 の導関数を必要とし、
の導関数を必要とし、
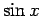 の導関数を導くには (1) が必要である、
の導関数を導くには (1) が必要である、
という構造、すなわち (1) を導くのに (1) が必要になってしまっているのが循環論法である、
という話である。
竹野茂治@新潟工科大学
2015年12月7日
![]() )」は、円の面積から定義するものではなく、
円の円周と直径の比として定義される:
)」は、円の面積から定義するものではなく、
円の円周と直径の比として定義される:
![]() に対しては、
に対しては、
![]() とすれば
とすれば
![]() となり、
となり、
![]() (ラジアン)、半径 1 の扇形で、
(ラジアン)、半径 1 の扇形で、
![]() OAC の代わりに
OAC の代わりに ![]() OBC (=
OBC (=![]() ) を使うこともあるが、
違いはほとんどない。
) を使うこともあるが、
違いはほとんどない。
になる、ということには、 円の面積の公式 (3) を使っていることになるが、 円の面積は (5) によって定義され、 それは (7) で見たように
の導関数を必要とし、
の導関数を導くには (1) が必要である、