しかし、![]() -
- ![]() 論法自身を具体的な問題で利用することも
可能だし、一見基本的な定理の利用や計算で証明できそうなものでも、
論法自身を具体的な問題で利用することも
可能だし、一見基本的な定理の利用や計算で証明できそうなものでも、
![]() -
- ![]() 論法を利用しないと証明が難しいものもある。
そのようなものを 2 つ程紹介する。
論法を利用しないと証明が難しいものもある。
そのようなものを 2 つ程紹介する。
まずは、関数 ![]()
![]() の連続性を証明する。
関数
の連続性を証明する。
関数 ![]() が
が ![]() で 連続 であるとは、
感覚的にはグラフがつながっていることを意味するが、
数学的には次の条件を満たすことである。
で 連続 であるとは、
感覚的にはグラフがつながっていることを意味するが、
数学的には次の条件を満たすことである。
![]() の定義域を
の定義域を ![]() とすれば (
とすれば (![]() は除いておく)、
定義域のすべての
は除いておく)、
定義域のすべての ![]() でもちろん
でもちろん ![]() の値は有限なので、
すべての
の値は有限なので、
すべての ![]() に対して、
に対して、
![]() -
- ![]() 論法からすると、証明すべきことは、
どんな
論法からすると、証明すべきことは、
どんな ![]() (
(![]() ) に対しても、
) に対しても、
まず、
![]() とする。そうしておけば、
とする。そうしておけば、
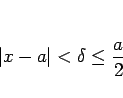
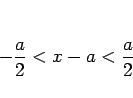
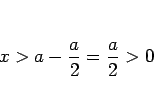
また、
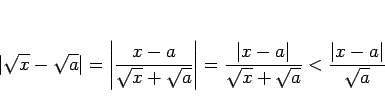
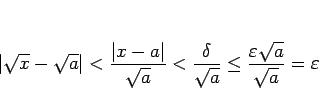
よって、どんな ![]() に対しても、
に対しても、
![]() を
を
![]() と
と ![]() の小さい方とすれば
(14) を満たすことができることがわかり、
(13) が言えたことになる。
の小さい方とすれば
(14) を満たすことができることがわかり、
(13) が言えたことになる。
次の命題は、一見基本的な定理の利用や計算で証明できそうなもので、
![]() -
- ![]() 論法を利用しないと証明が難しいものの一つである。
論法を利用しないと証明が難しいものの一つである。
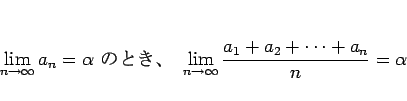
証明は煩雑なので紹介しないが、
興味があるならば参考文献 [1] を参照するといいだろう。