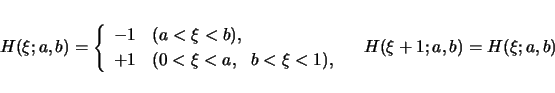

Next: 4 周期解の構造に関する実験
Up: 単独保存則方程式の周期解の数値解析 II
Previous: 2 粘性方程式の周期解
(PDF ファイル: kiyou2003.pdf)
3 周期解の個数
次に,非粘性方程式の周期解の集合の構造について考察する.
周期解は,外力と,周期毎に保存される値である初期平均値
に関して一意的には決まらないことが,
倍周期性を保証する定理 1 と,
外力と同じ周期を持つ周期解の存在を保証する結果[1]
に関する簡単な考察からわかる.
例えば 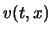 が,方程式 (1) の,
平均値
が,方程式 (1) の,
平均値 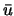 を持つ 2 倍周期解であるとする.
を持つ 2 倍周期解であるとする.
一方で,同じ平均値 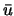 を持ち,外力と同周期の周期解
を持ち,外力と同周期の周期解 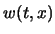 の
存在が保証されている.
の
存在が保証されている.
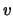 ,
,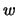 はもちろん等しくはないが,
はもちろん等しくはないが,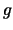 の周期を
の周期を 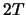 と見れば,
この 2 つは同じ平均値を持ち,外力の周期
と見れば,
この 2 つは同じ平均値を持ち,外力の周期 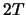 と同じ周期を持つ
周期解になっている.よって,周期外力,および平均値
と同じ周期を持つ
周期解になっている.よって,周期外力,および平均値 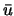 だけで周期解は一意には決まらないことになる.
だけで周期解は一意には決まらないことになる.
ここから,一つの外力と一つの平均値 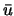 に対して,
はたしてどれくらいの数の周期解が存在するのかという疑問が起こるが,
前回の報告[4]の 5 節の例がはからずも
その答えを与えていることがわかった.
その例を,平行移動し構造を簡単にしたもので紹介する.
に対して,
はたしてどれくらいの数の周期解が存在するのかという疑問が起こるが,
前回の報告[4]の 5 節の例がはからずも
その答えを与えていることがわかった.
その例を,平行移動し構造を簡単にしたもので紹介する.
外力が
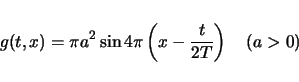 |
(4) |
の場合 (周期 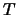 ),方程式 (1) は
次のような
),方程式 (1) は
次のような 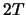 周期を持つ滑らかな周期解を持つ (Fig. 1).
周期を持つ滑らかな周期解を持つ (Fig. 1).
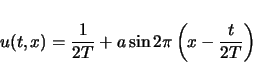 |
(5) |
一方で,以下の関数が任意の実数 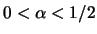 に対して,
同じ平均値
に対して,
同じ平均値 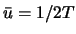 を持つ周期
を持つ周期 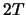 (
(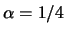 なら周期
なら周期 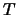 )
の不連続周期解であることを容易に検証できる (Fig. 2).
)
の不連続周期解であることを容易に検証できる (Fig. 2).
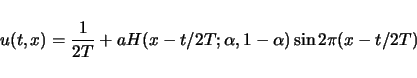 |
(6) |
ここで,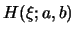 は,以下のような周期 1 の符号関数とする.
は,以下のような周期 1 の符号関数とする.
なお,不連続な部分も含む関数が保存則方程式の解であるためには,
滑らかな部分が方程式を満たすこと以外に,
不連続な部分が Rankine-Hugoniot 条件,
およびエントロピー条件と呼ばれる条件を満たす必要がある[2].
この例は,一つの外力と一つの平均値に対する周期解が,
少なくとも 1 パラメータの自由度を持つ程度に存在し得ることを示している.


Next: 4 周期解の構造に関する実験
Up: 単独保存則方程式の周期解の数値解析 II
Previous: 2 粘性方程式の周期解
Shigeharu TAKENO
2003年 11月 6日
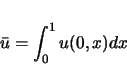
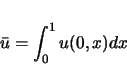
![]() が,方程式 (1) の,
平均値
が,方程式 (1) の,
平均値 ![]() を持つ 2 倍周期解であるとする.
を持つ 2 倍周期解であるとする.
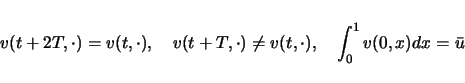
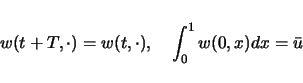
![]() に対して,
はたしてどれくらいの数の周期解が存在するのかという疑問が起こるが,
前回の報告[4]の 5 節の例がはからずも
その答えを与えていることがわかった.
その例を,平行移動し構造を簡単にしたもので紹介する.
に対して,
はたしてどれくらいの数の周期解が存在するのかという疑問が起こるが,
前回の報告[4]の 5 節の例がはからずも
その答えを与えていることがわかった.
その例を,平行移動し構造を簡単にしたもので紹介する.