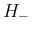
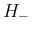 の
の
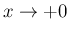 の評価を考える。
なお、この場合は
の評価を考える。
なお、この場合は 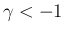 の拡張版に対しても考える必要がある。
の拡張版に対しても考える必要がある。
まず、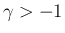 の場合を考える。
この場合は、以下の反転公式が利用できる。
の場合を考える。
この場合は、以下の反転公式が利用できる。
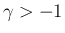 ,
, 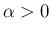 に対し次が成り立つ。
に対し次が成り立つ。
証明
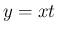 の置換積分により、
の置換積分により、
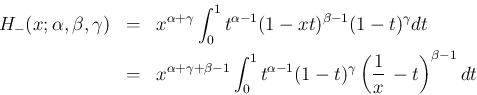
この補題 3 と前節の評価 (17) により、
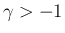 のときは
のときは
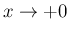 に対して
に対して
次は 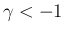 の場合を考える。
まずは、
の場合を考える。
まずは、
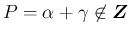 と仮定する。
ここで、
と仮定する。
ここで、
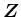 は整数全体の集合とする。
この場合、
は整数全体の集合とする。
この場合、
![$\gamma=[\gamma]+(\gamma)=-m+(\gamma)$](img93.png) とすると
とすると 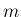 は 2 以上の整数で、
は 2 以上の整数で、
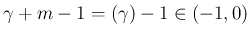 となるので
補題 2 を用いて
となるので
補題 2 を用いて 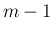 回リフティングすると、
回リフティングすると、
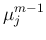 は
で、
は
で、
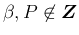 より 0 にはならないので、
(20), (21) より
より 0 にはならないので、
(20), (21) より 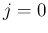 の項が
最低次になり、よって
となる。
の項が
最低次になり、よって
となる。
ここで、
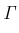 関数と
関数と
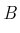 関数の拡張 (解析接続) を考える。
関数の拡張 (解析接続) を考える。
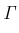 関数、
関数、
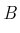 関数は通常は
関数は通常は
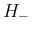 と同様に、
と同様に、
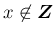 であれば
であれば 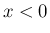 に対しても
に対しても
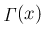 は
は
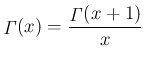
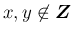 であれば
であれば 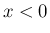 ,
, 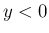 に
対しても
に
対しても
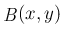 は (26) により
拡張できる。なお、これらの拡張は「解析接続」としてよく知られている。
また、以後
は (26) により
拡張できる。なお、これらの拡張は「解析接続」としてよく知られている。
また、以後
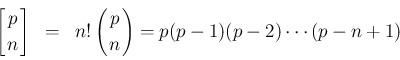
これらを利用すれば (23) の係数は、
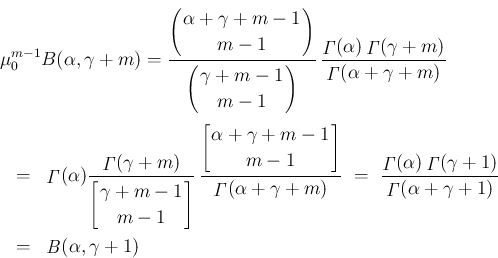
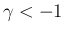 で
で
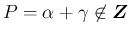 ならば
となり、式の上では
ならば
となり、式の上では 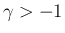 の場合の (19) と
同形となる。
の場合の (19) と
同形となる。
次は 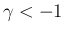 ,
,
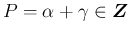 の場合を考える。
まず、
の場合を考える。
まず、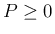 ならば、
ならば、
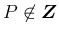 の場合の計算の (22) の
の場合の計算の (22) の 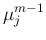 は、
は、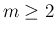 より 0 には
ならないので
より 0 には
ならないので
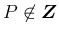 の場合の議論がそのまま使えて、
の場合の議論がそのまま使えて、
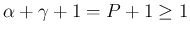 よりやはり (27) が
成立することになる。よって、あとは
よりやはり (27) が
成立することになる。よって、あとは 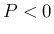 の場合を考えればよい。
の場合を考えればよい。
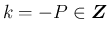 とすると
とすると 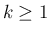 で、
で、
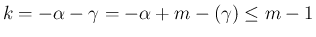 なので、
なので、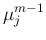 は
は
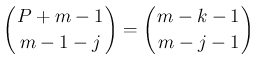
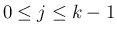 に対しては 0 になり、
それ以外の
に対しては 0 になり、
それ以外の 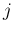 に対しては 0 ではない。よって、
に対しては 0 ではない。よって、
![\begin{eqnarray*}[0,0,0]_{-}
&=&
\frac{1}{x^{m-1}}\sum_{j=k}^{m-1}\mu^{m-1}_j[...
...\\ &=&
x^{\alpha+k+\gamma}(\mu^{m-1}_kB(\alpha+k,\gamma+m)+o(1))\end{eqnarray*}](img134.png)
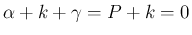 となるので
となるので
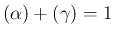 で、
となる。ここで、
で、
となる。ここで、
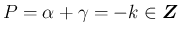 より、
より、
![$\displaystyle \gamma+m = (\gamma) = 1-(\alpha),
\hspace{1zw}\alpha+k = -\gamma = -[\gamma]-(\gamma) = m-1+(\alpha)
$](img139.png)
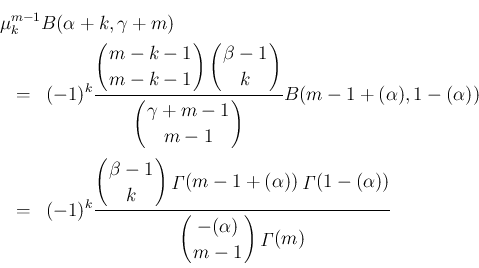
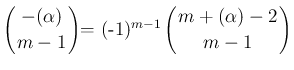
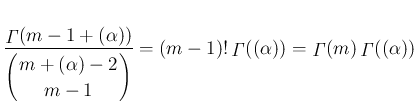
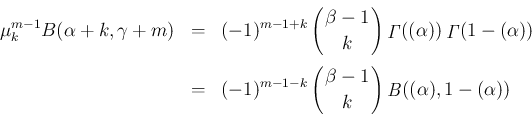
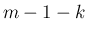 は
は
![$\displaystyle m-1-k=-[\gamma]-1+\alpha+\gamma=(\gamma)-1+\alpha=\alpha-(\alpha)
=[\alpha]
$](img145.png)
以上をまとめると、
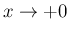 の場合は、
の場合は、
よって、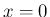 の近くでは、
の近くでは、
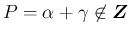 の場合は、
の場合は、
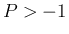 のとき、
のとき、
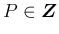 の場合はすべての場合で
の場合はすべての場合で 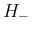 は
可積分となり、
また
は
可積分となり、
また
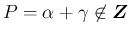 の場合は、
の場合は、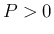 のとき、
のとき、
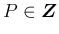 の場合はすべての場合で
の場合はすべての場合で 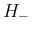 は有界となる。
は有界となる。
竹野茂治@新潟工科大学