B Helly の選出定理
この節では、Helly の選出定理 6.1 の証明を行う。
まず、系 A.2, A.5 より、
となる。
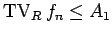 の仮定より、
の仮定より、
![\begin{displaymath}
0\leq P_{(-\infty,x]}f_n\leq A_1,
\hspace{1zw}
0\leq N_{(-\infty,x]}f_n\leq A_1\end{displaymath}](img874.gif) |
(B.144) |
なので、
まず一様有界な単調増加関数列 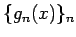 に対して収束性を示し、
それを
に対して収束性を示し、
それを
![$P_{(-\infty,x]}f_n$](img876.gif) ,
,
![$N_{(-\infty,x]}f_n$](img877.gif) に適用することで
に適用することで
 に対して示す、という方針で証明する。
に対して示す、という方針で証明する。
まず、 は
は
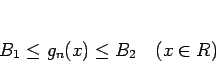
を満たし、かつ単調増加であるとする。
今、有理数全体を 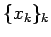 とすると
とすると
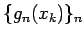 は有界列だから
その部分列を取ってある実数に収束させることができる。
よって、対角線論法を使うことで、
すべての
は有界列だから
その部分列を取ってある実数に収束させることができる。
よって、対角線論法を使うことで、
すべての 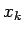 に対し収束するような
に対し収束するような 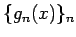 の部分列
の部分列
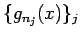 を取ることができる:
を取ることができる:
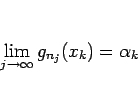
今、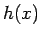 を
を
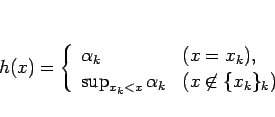
と定めると、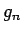 の単調性より
の単調性より 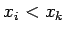 ならば
ならば
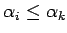 なので、
なので、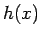 は単調増加であり、
かつ
は単調増加であり、
かつ
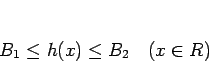
を満たす。
よって、命題 A.4 より 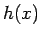 の不連続点の集合
の不連続点の集合 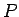 は
高々可算な集合である。
は
高々可算な集合である。
今、
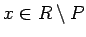 とすると、
とすると、
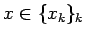 ならば
ならば
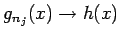 であるが、
であるが、
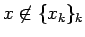 の場合も
の場合も
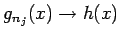 となることを示そう。
となることを示そう。
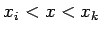 に対し、
に対し、
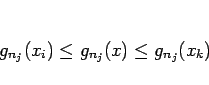
であるから、
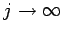 とすれば
とすれば
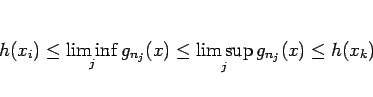
となるが、
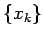 は稠密なので
は稠密なので 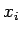 ,
, 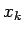 を
を 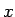 に収束するように取ると、
に収束するように取ると、
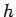 は
は 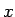 で連続だから
で連続だから 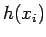 ,
, 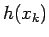 は
は 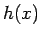 に収束し、
に収束し、
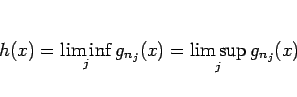
となり、よって確かに
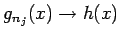 となる。
となる。
つまり、
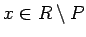 ならば
ならば
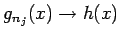 となるが、
となるが、
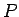 は高々可算集合で
は高々可算集合で 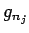 は一様有界なので、
は一様有界なので、
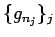 の部分列
の部分列
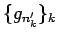 を取ることで
を取ることで
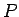 上でも
上でも 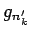 を収束させることができる。
よってその極限を
を収束させることができる。
よってその極限を
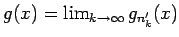 とすれば、
すべての
とすれば、
すべての 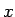 に対して
に対して 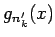 は
は 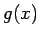 に収束することになる。
これで
に収束することになる。
これで 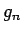 に対する収束性が示された。
に対する収束性が示された。
この議論と (B.3) により、
自然数列のある部分列 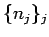 を取って、
関数列
を取って、
関数列
![$\{P_{(-\infty,x]}f_{n_j}\}_j$](img912.gif) ,
,
![$\{N_{(-\infty,x]}f_{n_j}\}_j$](img913.gif) と数列
と数列
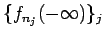 を
すべての
を
すべての 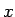 に対し各点収束させることができる。
その極限を、
に対し各点収束させることができる。
その極限を、
![\begin{displaymath}
\lim_{j\rightarrow\infty}P_{(-\infty,x]}f_{n_j}=g_1(x),
\hsp...
...,
\hspace{1zw}
\lim_{j\rightarrow\infty}f_{n_j}(-\infty)=\beta
\end{displaymath}](img915.gif)
とすると、(B.2) より、
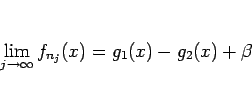
となる。よってこの右辺を
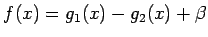 とすると
とすると
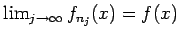 であり、
定理 6.1 の仮定より
であり、
定理 6.1 の仮定より
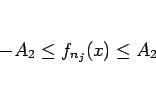
なので、
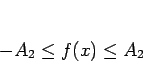
が従う。最後に 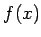 の全変動であるが、
これは (B.3) より
の全変動であるが、
これは (B.3) より
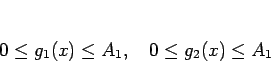
であり、かつ 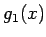 ,
, 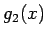 は単調なので、
は単調なので、
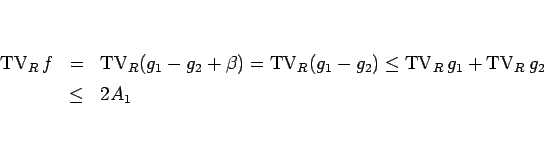
となる。これで定理 6.1 が示されたことになる。
竹野茂治@新潟工科大学
2009年1月18日
![]() は
は
![]() とすると、
とすると、
![]() ならば
ならば
![]() であるが、
であるが、
![]() の場合も
の場合も
![]() となることを示そう。
となることを示そう。
![]() に対し、
に対し、
![]() ならば
ならば
![]() となるが、
となるが、
![]() は高々可算集合で
は高々可算集合で ![]() は一様有界なので、
は一様有界なので、
![]() の部分列
の部分列
![]() を取ることで
を取ることで
![]() 上でも
上でも ![]() を収束させることができる。
よってその極限を
を収束させることができる。
よってその極限を
![]() とすれば、
すべての
とすれば、
すべての ![]() に対して
に対して ![]() は
は ![]() に収束することになる。
これで
に収束することになる。
これで ![]() に対する収束性が示された。
に対する収束性が示された。
![]() を取って、
関数列
を取って、
関数列
![]() ,
,
![]() と数列
と数列
![]() を
すべての
を
すべての ![]() に対し各点収束させることができる。
その極限を、
に対し各点収束させることができる。
その極限を、