4.3 相互作用がある場合
次は近づく波が含まれ、相互作用がある場合を考える。
以後、この節では簡単のため、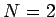 の場合に限定して証明を行う。
一般の
の場合に限定して証明を行う。
一般の 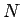 の場合の証明は、[Yong], [Dafermos] などを参照のこと。
の場合の証明は、[Yong], [Dafermos] などを参照のこと。
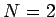 の場合は、
の場合は、
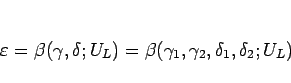 |
(4.37) |
であり、これを 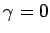 ,
, 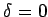 に関してテイラー展開する。
に関してテイラー展開する。
まず、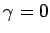 のときは
のときは
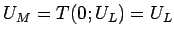 なので、
なので、
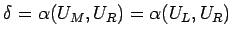 となり、
よって、
となり、
よって、
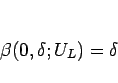 |
(4.38) |
となる。また、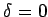 のときは、
のときは、
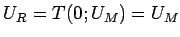 なので、
なので、
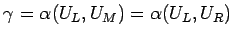 より
より
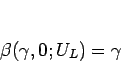 |
(4.39) |
であることがわかる。
よって、(4.8) を展開すると
その 1 次の項は 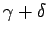 となる。
そして、(4.9), (4.10) より
となる。
そして、(4.9), (4.10) より
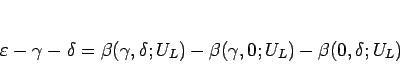
と書けるが、この右辺を次のように分ける:
| 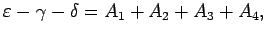 |
| 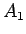 |
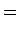 |
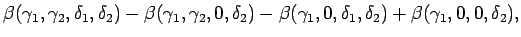 |
(4.41) |
| 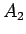 |
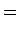 |
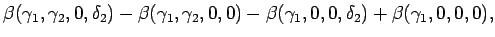 |
(4.42) |
| 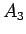 |
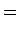 |
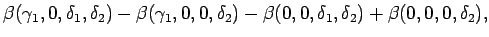 |
(4.43) |
| 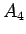 |
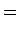 |
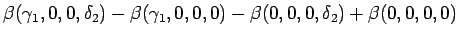 |
(4.44) |
しかし、
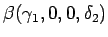 の波はすべて近づかないので、
補題 4.3 より、
の波はすべて近づかないので、
補題 4.3 より、
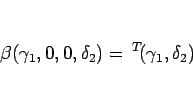
となり、よって
(4.9), (4.10) より 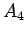 は
は
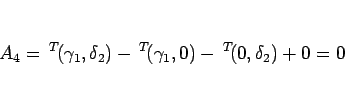 |
(4.45) |
となる。
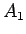 は、
は、
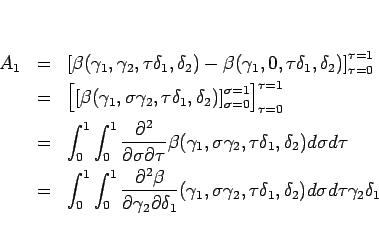
と変形できるので、
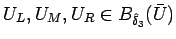 に対して、
に対して、
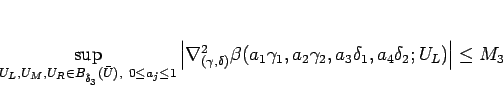
とすると、
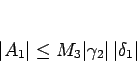 |
(4.46) |
と評価できる。
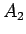 は、
は、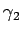 と
と 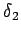 が近づかなければ、
補題 4.3 より
が近づかなければ、
補題 4.3 より
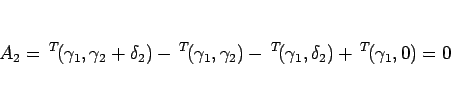 |
(4.47) |
であり、近づく場合は 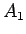 と同様に
と同様に
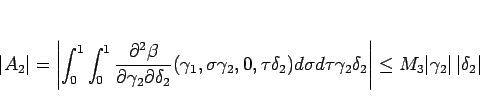 |
(4.48) |
となる。同様に 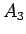 も、
も、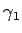 と
と 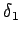 が近づかなければ、
が近づかなければ、
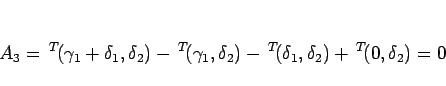 |
(4.49) |
近づく場合は、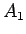 と同様に
と同様に
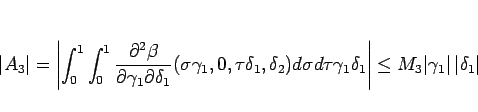 |
(4.50) |
となるので、
(4.11),(4.16),
(4.17),
(4.18), (4.19),
(4.20), (4.21)
により、結局定理 4.1 が得られることになる。
なお、[Yong] には
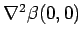 を求めることにより、
(4.1) よりも詳しい評価式
を求めることにより、
(4.1) よりも詳しい評価式
が示されている。
この (4.22) によれば、
2 次の項は 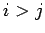 の波の相互作用のみであり、
の波の相互作用のみであり、
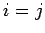 で近づく波 (同じ特性方向の波) の相互作用の影響は
実際には 3 次以上の項であることがわかる。
で近づく波 (同じ特性方向の波) の相互作用の影響は
実際には 3 次以上の項であることがわかる。
竹野茂治@新潟工科大学
2009年1月18日
![]() の場合は、
の場合は、
![]() のときは
のときは
![]() なので、
なので、
![]() となり、
よって、
となり、
よって、
![]() は、
は、
![]() は、
は、![]() と
と ![]() が近づかなければ、
補題 4.3 より
が近づかなければ、
補題 4.3 より
![]() を求めることにより、
(4.1) よりも詳しい評価式
を求めることにより、
(4.1) よりも詳しい評価式