5 空間周期的な場合の減衰評価
この節では、問題 2 の空間周期的な解 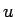 の
時間方向の減衰を考える。
の
時間方向の減衰を考える。
まず、
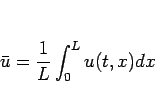
は 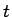 によらない定数であることに注意する。
それは、(2)、
および
によらない定数であることに注意する。
それは、(2)、
および 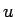 (よってもちろん
(よってもちろん 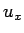 も) の周期性により
も) の周期性により
![\begin{eqnarray*}\lefteqn{\frac{d}{dt}\int_0^L u(t,x)dx
=\int_0^L u_t(t,x)dx
...
...dx}
\ &=&
\left[-f(u)+\varepsilon u_x\right]_{x=0}^{x=L}
=
0\end{eqnarray*}](img84.gif)
となるからである。
この 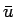 は
は 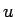 の平均値であり、
の平均値であり、
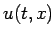 はこの
はこの 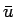 に向かって減衰する。
ここでは、定理 2 を用いてそれを示す。
に向かって減衰する。
ここでは、定理 2 を用いてそれを示す。
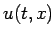 は滑らかであり
は滑らかであり 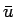 は平均値であるから、
各
は平均値であるから、
各 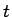 に対して
に対して
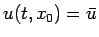 となる
となる 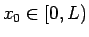 が存在する。
よって、
が存在する。
よって、![$x\in [0,L]$](img88.gif) に対して、
に対して、
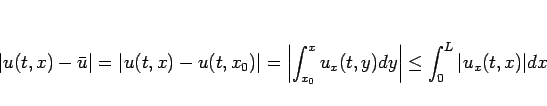 |
(16) |
となる。
今、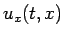 の正の部分を
の正の部分を 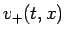 、負の部分を
、負の部分を 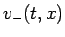 とする。
とする。
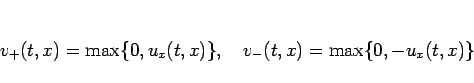 |
(17) |
すると、
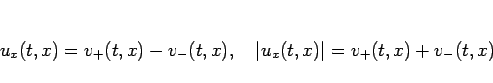
であり、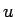 の周期性により
の周期性により
![\begin{displaymath}
\int_0^L u_x(t,x)dx=\left[u(t,x)\right]_{x=0}^{x=L}=0
\end{displaymath}](img95.gif)
なので、
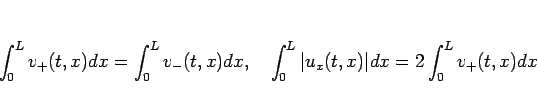 |
(18) |
が言える。定理 2 により
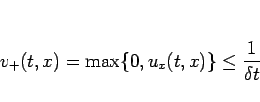 |
(19) |
であるので、
(16), (18), (19) より
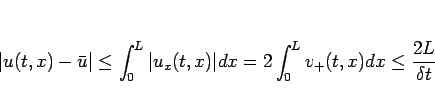
が得られる。
定理 3
問題 2 の場合、
(2) の解 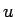 は
は 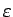 に一様に
次の減衰評価を満たす。
に一様に
次の減衰評価を満たす。
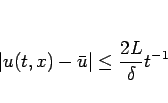 |
(20) |
竹野茂治@新潟工科大学
2009年1月25日
![]() は滑らかであり
は滑らかであり ![]() は平均値であるから、
各
は平均値であるから、
各 ![]() に対して
に対して
![]() となる
となる ![]() が存在する。
よって、
が存在する。
よって、![]() に対して、
に対して、
![]() の正の部分を
の正の部分を ![]() 、負の部分を
、負の部分を ![]() とする。
とする。
![]() は
は ![]() に一様に
次の減衰評価を満たす。
に一様に
次の減衰評価を満たす。