![$\displaystyle
\left[\begin{array}{c}\rho\\ m\end{array}\right]_t + \left[\begi...
...rho+P(\rho)\end{array}\right]_x = \left[\begin{array}{c}0\\ 0\end{array}\right]$](img11.png) (2)
(2)
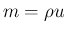 (気体の運動量) とした。
(気体の運動量) とした。
一般に、次の形の方程式を、1 次元保存則方程式 と呼ぶ。
ここで、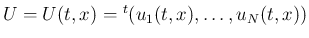 は
は 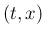 2 変数の
2 変数の 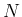 次元ベクトル値の未知関数、
次元ベクトル値の未知関数、
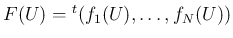 は
は
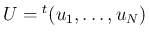 に関して滑らかな
に関して滑らかな 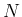 次元ベクトル関数で、
次元ベクトル関数で、
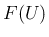 自体 (
自体 (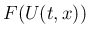 ではなく) は既知とする。
例えば、(2) では、
ではなく) は既知とする。
例えば、(2) では、
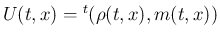 ,
,
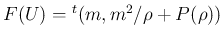 である。
である。
この 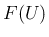 の
の 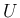 に関する勾配 (
に関する勾配 (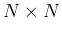 行列)
行列)
![\begin{displaymath}
\nabla_U F(U) = \left[
\begin{array}{ccc}
\displaystyle \...
...laystyle \frac{\partial f_N}{\partial u_N}
\end{array}\right]
\end{displaymath}](img25.png)
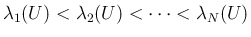 を持つ場合、保存則方程式 (3) は 双曲型 と呼ばれる。
を持つ場合、保存則方程式 (3) は 双曲型 と呼ばれる。
本稿では、(1) の圧力 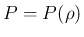 は
以下の条件 (4), (5) を
満たすとする。
は
以下の条件 (4), (5) を
満たすとする。
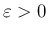 に対して
なお、(4), (5) により、
自然に
に対して
なお、(4), (5) により、
自然に 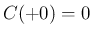 となる (A 節参照)。
ポリトロピック、すなわち
となる (A 節参照)。
ポリトロピック、すなわち
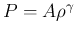 の場合は、
(4) の条件は
の場合は、
(4) の条件は 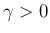 に対応し、
(5) の条件は
に対応し、
(5) の条件は 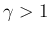 (等エントロピー的) に対応する。
今後、
(等エントロピー的) に対応する。
今後、
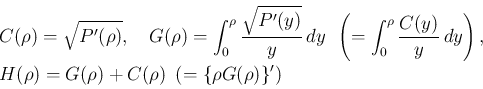
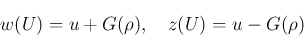
(2) に関する 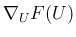 は
は
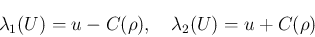
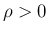 では (2) は双曲型となる。
なお、この
では (2) は双曲型となる。
なお、この 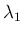 ,
, 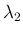 を使うと、(8) は
と書くこともできる。
を使うと、(8) は
と書くこともできる。
竹野茂治@新潟工科大学