整列化に必要な手順数は、A 列の増加列ブロック数によって決まり、
命題 1, 3,
6, 7 より、
![]() のとき、
のとき、
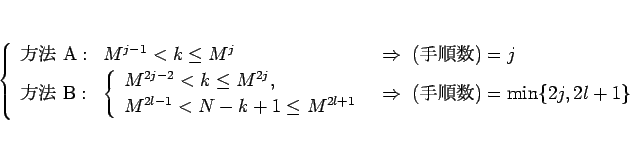
例えば、![]() ,
, ![]() の場合は
の場合は
| 1 | 2 | 3 | 4 | 5 | |
| 0 | 1 | 2 | 2 | 3 | |
| 0 | 2 | 2 | 2 | 4 | |
| 3 | 3 | 3 | 1 | 1 | |
| 0 | 2 | 2 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | |
| 0 | 2 | 2 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 5 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | |
| 0 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 1 | 1 |
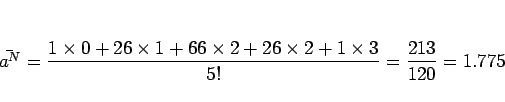
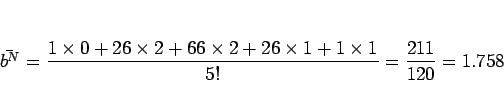
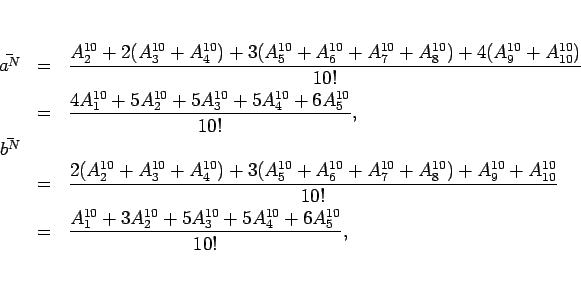
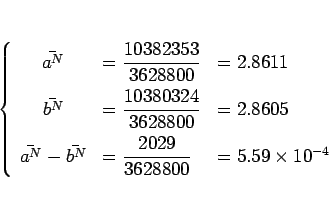
同様に、
![]() での値をコンピュータに数値計算させた結果は
以下の通りである。
での値をコンピュータに数値計算させた結果は
以下の通りである。
| 10 | 20 | 50 | 100 | |
| 2.8611 | 3.9390 | 5.000 | 6.000 | |
| 2.8605 | 3.9390 | 5.000 | 6.000 | |
|
|
|
|
|
|
なお、この表に見られるように、この差は ![]() に関して単調減少ではない。
それについては今後さらに調べてみたいと思う。
に関して単調減少ではない。
それについては今後さらに調べてみたいと思う。
また、![]() のようにかなり大きな
のようにかなり大きな ![]() に対する
に対する ![]() の計算は
実はコンピュータでも容易ではなく、
計算式としては (4), (5) の
どちらを使っても、
それらの式を普通に計算すると桁落ちなどによるものと思われる
誤差が大きく発生してしまう。
の計算は
実はコンピュータでも容易ではなく、
計算式としては (4), (5) の
どちらを使っても、
それらの式を普通に計算すると桁落ちなどによるものと思われる
誤差が大きく発生してしまう。
例えば、![]() の (4), (5) の
最初の項である
の (4), (5) の
最初の項である ![]() は
は
![]() より 170 桁であるが、
実際の
より 170 桁であるが、
実際の ![]() は 158 桁しかなく、
つまり (4), (5) の
第 2 項目以降の項による引き算により上位の桁が下がってしまう。
単純な倍精度計算で計算したところ、
本来は 1 になるべき
は 158 桁しかなく、
つまり (4), (5) の
第 2 項目以降の項による引き算により上位の桁が下がってしまう。
単純な倍精度計算で計算したところ、
本来は 1 になるべき
![]() の値が
1 を大きく超えてしまった。
の値が
1 を大きく超えてしまった。
このような場合、桁落ちが起きないような、同符号のみの項からなるような 計算式を求めるか、あるいは多倍長演算を行なう、などの必要があるが、 今回は 170 桁の多倍長整数演算を用いて (4) により 計算を行なった。 しかし、同符号のみの項による展開式があれば計算は容易になるはずなので、 それについても今後考えてみたいと思う。