次へ: 6 最適解の構成 上へ: sort1 前へ: 4 A 列と B 列 (PDF ファイル: sort1-2.pdf)

5 必要な回数の評価

A 列の配分によって、何が起こるかを考えてみる。 例えば、$N=6$ のものを 1 回配分してみる。

$$1 2 3 4 5 6 \rightarrow \left\{\begin{array}{ll} A_... ...1 3 6\end{array}\right. \rightarrow (2 4 5), (1 3 6)$$

この例からもわかるように、 A 列はそれぞれの山への配分により 2 つのグループに分けられ、 それをまとめて作った結果の列は、各グループだった部分は必ず増加列であり、 減少するところは、そのグループの切れ目でのみ起こることになる。

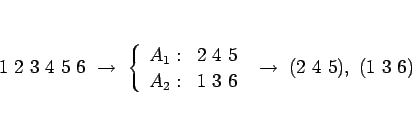
もう 1 回これを配分すると、次のようになる:

$$\begin{array}{l} (\mbox{1 回目 $A_1$}), (\mbox{1 回目 $A_2... ... 回目 $A_1$, 2 回目 $A_2$ だった 部分を意味する}) \end{array}$$

一般には 2 回の手順によりこのような 4 ブロックに分かれるが、 実際にはそのうちいくつかは空集合で、 3 ブロック以下であることも起こりうる。

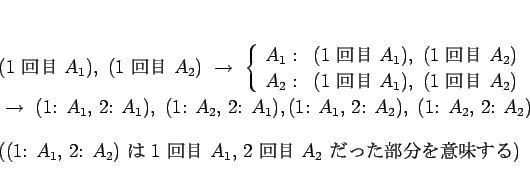
このように考えると、 「$k$ 回配分した後では、 A 列には最高 $2^k$ 個の増加列のブロック、 (すなわち $(2^k-1)$ 箇所の減少箇所) ができることになる」、 ということがわかる。これは言いかえれば、 「$(k-1)$ 回の手順では $2^{k-1}$ 個の増加列ブロックしか作られない」、 ということも言えるから、結局次が言えることになる。

命題 1

A 列の最終列に含まれる増加列のブロック数が ($2^{k-1}+1$) 個以上ならば、 少なくとも $k$ 回の手順が必要。

$M>2$ の場合は、この ($2^{k-1}+1$) を ($M^{k-1}+1$) で置きかえれば 同じことが言える。

また、容易に次も言える。

系 2

$M^{k-1}<N\leq M^k$ のとき、 少なくとも $k$ 回の手順が必要となる B 列の初期配列が存在する。

証明

これは、丁度逆順の B 列の初期配置 $N$,$(N-1)$,...,3,2,1 が それに相当する。 この B 列の初期配置に対しては、A 列の最終配置も丁度逆順の $N$,$(N-1)$,...,3,2,1 なので、 増加列のブロックは $N$ 個あることになる。 仮定より $N\geq M^{k-1}+1$ だから命題 1 より 少なくとも $k$ 回の手順が必要。

次へ: 6 最適解の構成 上へ: sort1 前へ: 4 A 列と B 列