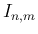
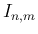 は、2 つの意味で広義積分となっていて、
ひとつは
は、2 つの意味で広義積分となっていて、
ひとつは
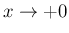 に関してであり、
もうひとつは
に関してであり、
もうひとつは
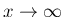 に関してである。
に関してである。
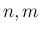 が整数の場合、
が整数の場合、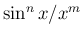 の
の
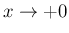 のオーダーは
のオーダーは 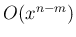 であるから、
であるから、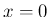 の近くで
リーマン広義積分の意味で積分できるためには、
の近くで
リーマン広義積分の意味で積分できるためには、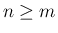 が必要かつ十分である。
が必要かつ十分である。
一方、
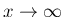 の方は、
の方は、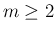 であれば
であれば
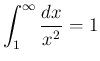
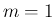 のときは少し面倒である。
のときは少し面倒である。
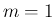 の場合、
の場合、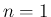 のときは前に述べたようにリーマン広義積分が存在して、
のときは前に述べたようにリーマン広義積分が存在して、
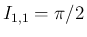 となることが知られているが、
その証明は易しくはない。例えば、
[7] IV 章 11 の章末問題にあるリーマン・ルベーグの定理を
使う方法、
[7] IV 章 14 の例 3 の 2 変数関数の微分と積分の順序交換を
利用する方法、
[8] IX 章 2 の例 5 の複素積分の留数の定理を
利用する方法などがある。
となることが知られているが、
その証明は易しくはない。例えば、
[7] IV 章 11 の章末問題にあるリーマン・ルベーグの定理を
使う方法、
[7] IV 章 14 の例 3 の 2 変数関数の微分と積分の順序交換を
利用する方法、
[8] IX 章 2 の例 5 の複素積分の留数の定理を
利用する方法などがある。
さらに、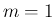 で
で 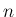 が奇数の場合も
が奇数の場合も 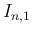 のリーマン広義積分は
有限値となるが、
のリーマン広義積分は
有限値となるが、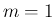 で
で 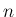 が偶数の場合は
リーマン広義積分は無限大に発散する。
ここでは、
が偶数の場合は
リーマン広義積分は無限大に発散する。
ここでは、
整数 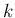 に対して、
に対して、
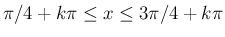 では
では
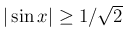 なので、
なので、
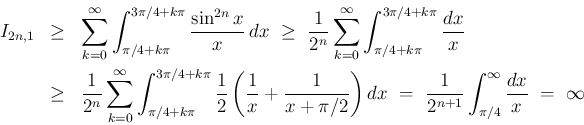
結局、広義積分 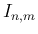 が有限値となるのは、
が有限値となるのは、
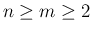 のとき
のとき
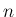 が奇数で
が奇数で 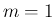 のとき
のとき
竹野茂治@新潟工科大学