![]() のすべての
のすべての ![]() に対して
に対して
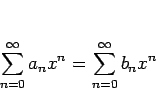
証明
![]() では絶対収束するので、両辺の差を考えると、
では絶対収束するので、両辺の差を考えると、
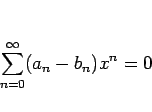
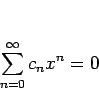
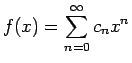 とおくと、
とおくと、
![]() で
で ![]() であり、
であり、![]() なのでまず
なのでまず ![]() が言える。
また、定理 12 により、
が言える。
また、定理 12 により、
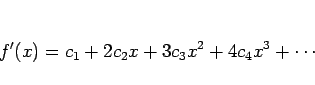
この定理により、微分や積分、![]() の積や商によって得られた級数や、
(13) のように
の積や商によって得られた級数や、
(13) のように ![]() の代わりに
の代わりに ![]() などを代入して
得られる級数が、
マクローリン展開の計算によって得られるものと
一致することが言えることになる。
例えば、
などを代入して
得られる級数が、
マクローリン展開の計算によって得られるものと
一致することが言えることになる。
例えば、
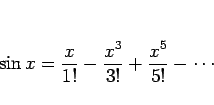
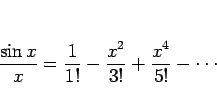
マクローリン展開と一致することは、より明確に次の形で与えられる。
![]() で
で
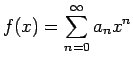 であるとき、
であるとき、
![]() となる。
となる。
証明
![]() は OK. 定理 12 より、
は OK. 定理 12 より、
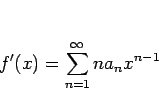
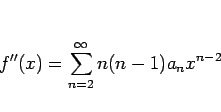
さらに、この命題 15 より奇関数、偶関数に関しては 次が言える。
![]() で
で
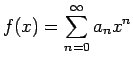 が、
が、
証明
![]() が奇関数のとき、
が奇関数のとき、![]() であるから、
これに
であるから、
これに ![]() を代入すると
を代入すると ![]() が得られる。
が得られる。
また、2 回微分すると
![]() であるから、
これに
であるから、
これに ![]() を代入して
を代入して ![]() が得られる。
同様にして
が得られる。
同様にして ![]() (
(
![]() ) が言える。
よって、系 15 より
) が言える。
よって、系 15 より ![]() となる。
となる。
偶関数の場合は ![]() であるから、
であるから、
![]() となり、よって
となり、よって ![]() となる。
以下同様に
となる。
以下同様に
![]() が言え、よって
が言え、よって ![]() が言える。
が言える。