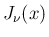
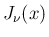 、ノイマン関数
、ノイマン関数 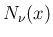 について、
次の漸化式が成り立つことがよく知られている (例えば [2] 38)。
また [2] によれば (39)、半ベッセル関数は
以下のように表されるようである。
この公式 (2) がを使えば、
とりあえずすべての半ベッセル関数を
について、
次の漸化式が成り立つことがよく知られている (例えば [2] 38)。
また [2] によれば (39)、半ベッセル関数は
以下のように表されるようである。
この公式 (2) がを使えば、
とりあえずすべての半ベッセル関数を 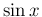 ,
, 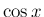 で表すことができるが、
(2) は商の関数の
で表すことができるが、
(2) は商の関数の 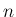 階微分、
しかも
階微分、
しかも 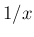 が微分の度にかけ算されるという公式なので、
大きい
が微分の度にかけ算されるという公式なので、
大きい 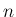 に対する計算はかなり手間がかかる。
に対する計算はかなり手間がかかる。
実際、これを用いて、最初の 3 つの微分の部分を計算してみると 以下のようになる。
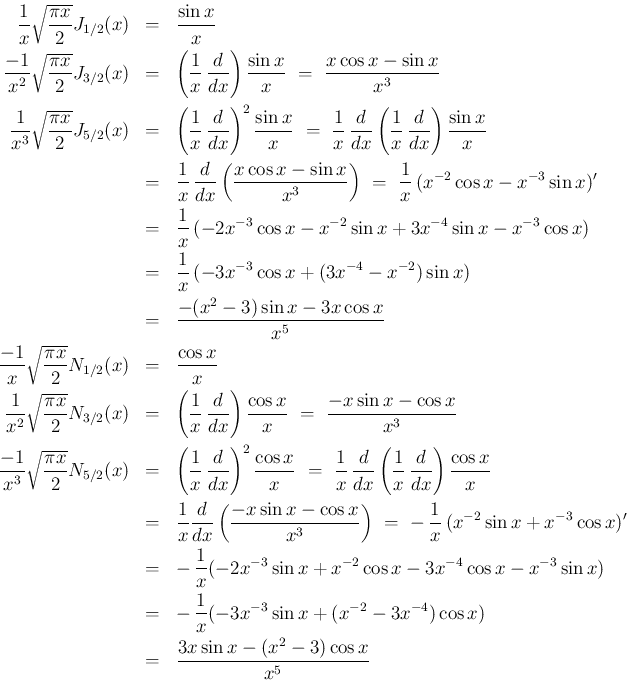
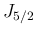 ,
, 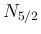 は、
公式 (2) で計算するよりも、
むしろ漸化式 (1) と 1/2, 3/2 次の関数を使って
計算する方が、微分の計算なしに代数計算だけで済む分易しい。
は、
公式 (2) で計算するよりも、
むしろ漸化式 (1) と 1/2, 3/2 次の関数を使って
計算する方が、微分の計算なしに代数計算だけで済む分易しい。
(2) の公式でも上の計算のように、 ひとつ前の計算を利用して次の次数が計算できるが、 やはり微分の計算は必要なので、 漸化式 (1) の代数計算に比べれば多少面倒である。
竹野茂治@新潟工科大学