8 f6(0)
この節では、7 節で考察した 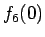 を求める。
以後この
を求める。
以後この 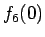 を
を
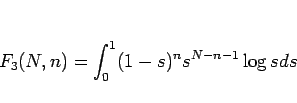 |
(21) |
のようにおいてこれを考えることにする。
なお、 で
で 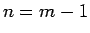 なので、
ここまでは
なので、
ここまでは 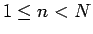 としてきたが、
この (21) を考える場合は
としてきたが、
この (21) を考える場合は 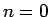 を除外する必要はないので、
この (21) は
を除外する必要はないので、
この (21) は 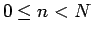 として考えることにする。
として考えることにする。
部分積分により、
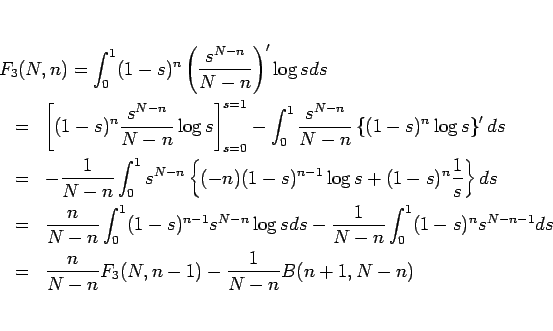
となるが、この第 2 項は、
既に 7 節の  の計算で見たように、
の計算で見たように、
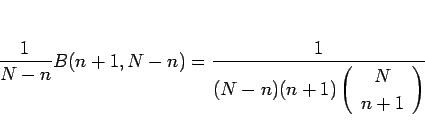
と書けるので、
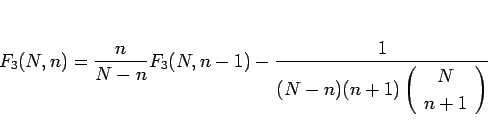
となり、両辺を 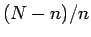 倍すれば、
倍すれば、
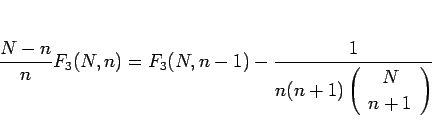 |
(22) |
となる。ここで、
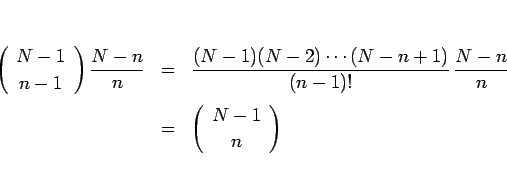
なので、(22) の両辺を
 倍すれば
倍すれば
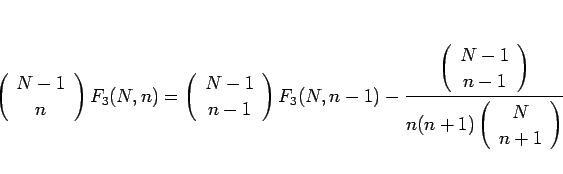
と書ける。
この最後の項は、
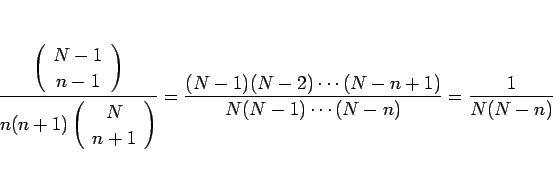
となるので、結局
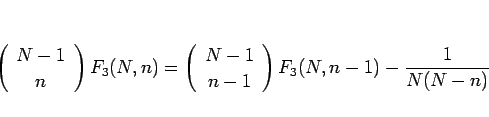
が成り立つことになる。
この右辺の最初の項は、左辺の 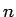 を
を 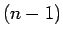 にした形になっているので
繰り返し代入すれば
にした形になっているので
繰り返し代入すれば
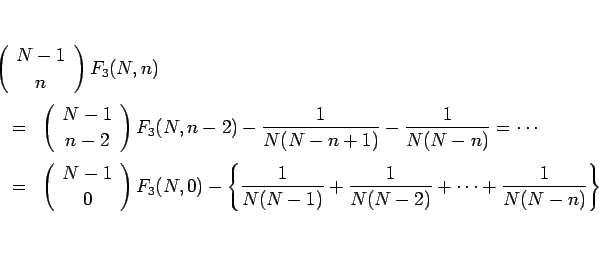
が得られる。ここで、
![\begin{displaymath}
F_3(N,0)
=
\int_0^{1}s^{N-1}\log sds
=
\left[\frac{s^N}{N}\l...
...s
=
-\left[\frac{s^N}{N^2}\right]_{s=0}^{s=1}
=
-\frac{1}{N^2}
\end{displaymath}](img200.gif)
なので、よって
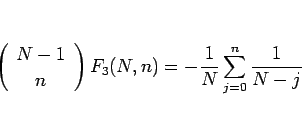
となり、結局 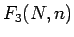 は
は
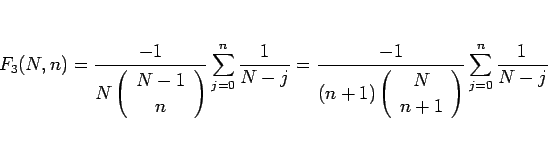
と表されることになる。よって (20) より、
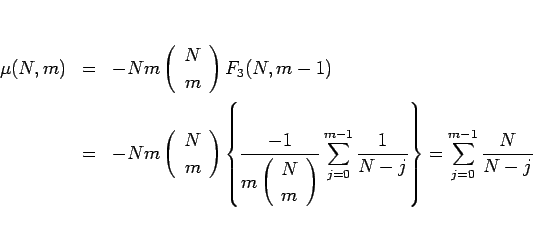
となり、これでようやく (3) と同じものが得られたことになる。
竹野茂治@新潟工科大学
2008年5月24日
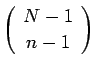 倍すれば
倍すれば