この問題では、一つ目はどれを選んでもいいので一つ目は必ず 1 回で決まる。 この先、次の二つ目 (2 種類目) の数字が出るまでに 平均何回かかるかを考えてみる。
この場合は、一つ目の同じものが出続けている間は選択し続けるが、 そうでないものが出ればそこで終わりである。 つまり、
1 回で済む確率のようになる。よって、二つ目の数字が出るまでの回数の期待値は、,
2 回で済む確率,
3 回で済む確率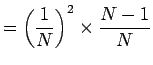
![]() 個の異なる数字が取れたところから始めると、
次の
個の異なる数字が取れたところから始めると、
次の ![]() 個目の異なる数字が取れるまでには、
個目の異なる数字が取れるまでには、
1 回で済む確率のようになるので、期待値は,
2 回で済む確率,
3 回で済む確率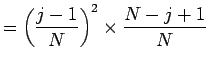
(3)
竹野茂治@新潟工科大学