3 一般化について
2 節では 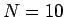 ,
, 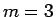 の場合について考察したが、
しかしこれを一般化するのは容易ではない。
例えば
の場合について考察したが、
しかしこれを一般化するのは容易ではない。
例えば 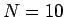 ,
, 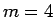 の場合を考えてみる。
の場合を考えてみる。
この場合、例えば 7 回で終わる (3 回余計にかかる) のは、
3 回分前に出ているものと同じものが 6 回目までに出る場合で、
それぞれの確率は、それまでに出ている数の個数に応じて 1/10, 2/10, 3/10 となる。
よって、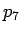 は、
は、
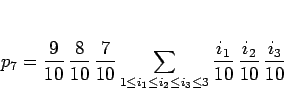
となる。この場合は、
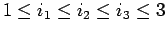 となるすべての
となるすべての
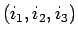 の組を上げて数えてみれば求められなくはないが、
一般には、
の組を上げて数えてみれば求められなくはないが、
一般には、
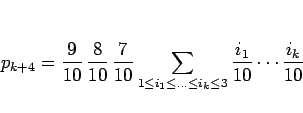
であり、この最後の和を求めるのは容易ではない。一応、
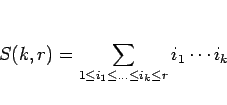
とすると、
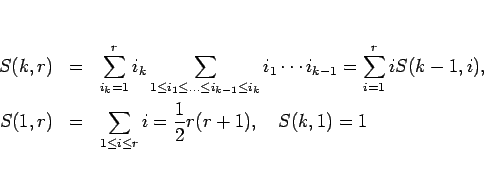
などの性質を用いれば、
小さい 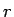 に対しては
に対しては 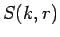 を順次決定できなくはないが、
かなり大変である (詳しくは 6 節を参照)。
を順次決定できなくはないが、
かなり大変である (詳しくは 6 節を参照)。
よって、一般の場合を考える場合は、別な方法をとる方がよい。
竹野茂治@新潟工科大学
2008年5月24日
![]() は、
は、