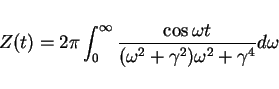

Next: 2 置換積分と部分分数分解
Up: ある定積分について
Previous: ある定積分について
(PDF ファイル: kusa1.pdf)
広義積分
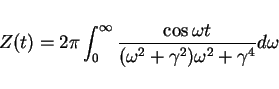 |
(1) |
について考えてみます。分母は 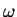 の 4 次式で因数分解して考えると
公式 (cf.[1])
の 4 次式で因数分解して考えると
公式 (cf.[1])
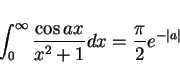 |
(2) |
が使えるのではないかと予想されるのですが、以下に述べるやや微妙な事情があり
注意が必要です。
- 広義積分は発散して無限大になることもあるので、簡単に和や差を行うことが
できず、常に個々の積分が有限であるかどうかを確認し、
例えば
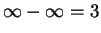 のような式にならないように注意する必要がある
のような式にならないように注意する必要がある
- 公式 (2) は数学辞典 [1] に載っているし、
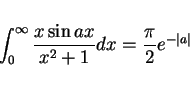 |
(3) |
という公式は載っているものの
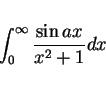 |
(4) |
に関する公式は載っていない
公式 (2),(3) はいずれも複素関数の留数計算などから
導かれるのですが、(4) はそれにはうまく載らない形で、
きれいな式で表すことはできない (あるいは知られていない) のではないかと
思われます。よってこの式が出てきたら、少なくとも私の手元の数学辞典
[1] よりもう少し詳しい公式集が必要かもしれませんし、
もしかしたら簡単な式で表すのは無理なのかも知れません。


Next: 2 置換積分と部分分数分解
Up: ある定積分について
Previous: ある定積分について
Shigeharu TAKENO
2003年 11月 27日