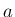
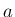 という一定間隔をあけた曲線を構成するため、
元の曲線に対する設定を行う。
という一定間隔をあけた曲線を構成するため、
元の曲線に対する設定を行う。
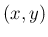 平面上の元の閉曲線を
平面上の元の閉曲線を 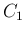 とし、
その上の点
とし、
その上の点
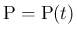 が以下のように表されているとする。
が以下のように表されているとする。
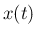 ,
, 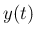 は十分滑らかで、
でかつ
は十分滑らかで、
でかつ
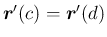 (始点と終点も滑らかにつながる) とする。
また、
(始点と終点も滑らかにつながる) とする。
また、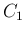 は交差のない閉曲線で、その内部に原点を含み、
は交差のない閉曲線で、その内部に原点を含み、
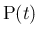 は
は 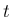 の増加にともない反時計回り、
すなわち
の増加にともない反時計回り、
すなわち 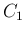 の内部を左に見ながら進むとする。
さらに、その曲率
は、正、すなわち
の内部を左に見ながら進むとする。
さらに、その曲率
は、正、すなわち 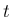 の増加に伴ない左方向に曲るか、
または負であってもその曲率半径
の増加に伴ない左方向に曲るか、
または負であってもその曲率半径 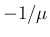 は
は 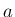 より大、すなわち、
が成り立つとする。
この条件により、
より大、すなわち、
が成り立つとする。
この条件により、 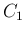 の外側に
の外側に 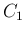 上の点 P で接するような半径
上の点 P で接するような半径 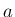 の
円を書いても、その円は
の
円を書いても、その円は 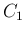 と P 以外では交わることはなく、
また
と P 以外では交わることはなく、
また 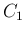 の点から
の点から 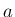 の長さの法線を
の長さの法線を 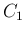 の外側に伸ばしても、
それが他の法線とぶつかることはないので、
の外側に伸ばしても、
それが他の法線とぶつかることはないので、
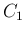 から
から 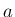 だけ離れた曲線を交差のない状態で
作ることができるようになる。
だけ離れた曲線を交差のない状態で
作ることができるようになる。
なお、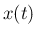 ,
, 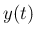 が十分滑らかと仮定したが、
それにより
が十分滑らかと仮定したが、
それにより 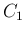 として正方形や多角形のような角のある閉曲線は
許されないことになるが、その角を小さく丸めることで、
それらに十分近いものは含まれる。
として正方形や多角形のような角のある閉曲線は
許されないことになるが、その角を小さく丸めることで、
それらに十分近いものは含まれる。
竹野茂治@新潟工科大学