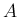
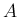 の行ベクトル
の行ベクトル
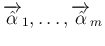 が線形従属の場合を考える。
結論から言えば、この場合は
が線形従属の場合を考える。
結論から言えば、この場合は
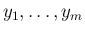 は独立にはならない。
本節はそのこと、すなわち (10) が
成り立つとして矛盾を示す。
は独立にはならない。
本節はそのこと、すなわち (10) が
成り立つとして矛盾を示す。
まず、すべての 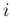 に対し
に対し
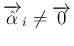 と
してよいことを示す。それは、もしある
と
してよいことを示す。それは、もしある 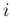 に対して
に対して
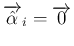 ならば
ならば 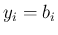 (定数) となるから、
(定数) となるから、
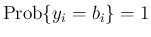 となって
となって 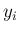 が連続確率変数ではないことに
なるからである。
が連続確率変数ではないことに
なるからである。
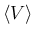 を
を 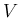 のベクトルが張るベクトル空間、
すなわち
のベクトルが張るベクトル空間、
すなわち 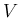 の有限個のベクトルの線形結合の全体 (
の有限個のベクトルの線形結合の全体 (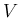 を含む最小の部分空間) とする。
を含む最小の部分空間) とする。
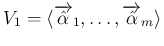 の
次元を
の
次元を 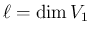 とすると、線形従属の仮定から
とすると、線形従属の仮定から 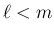 で、
で、
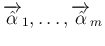 から
線形独立な
から
線形独立な 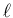 個のベクトルを取ることができる。
個のベクトルを取ることができる。
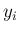 の添字の順序を変えることで、その
の添字の順序を変えることで、その 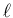 個のベクトルを
個のベクトルを
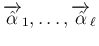 とする
ことができ、残りの
とする
ことができ、残りの
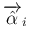 (
(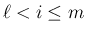 ) は
すべて
) は
すべて
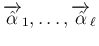 の
線形結合として書ける、すなわち
の
線形結合として書ける、すなわち
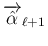 は、
の形に書ける。
は、
の形に書ける。
まず、(10) が成り立つとき、
その 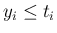 のいくつかを
のいくつかを 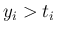 に
変えることができることに注意する。
例えば (10) で
に
変えることができることに注意する。
例えば (10) で
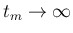 とすると
とすると
(18) の係数の 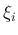 を正のもの、負のもの、
0 のものに分類する。
を正のもの、負のもの、
0 のものに分類する。
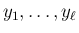 の順序を交換すれば、
の順序を交換すれば、
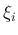 の順序が変わるので、
の順序が変わるので、
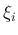 はすべてが 0 にはならないから、
はすべてが 0 にはならないから、
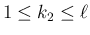 である。
である。
これに合わせて、(10) の不等式
のうち 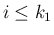 の部分を逆向きに変え、
さらに
の部分を逆向きに変え、
さらに
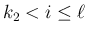 の部分、
および
の部分、
および
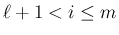 の部分は
の部分は
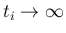 と
することでその不等式を消して、
と
することでその不等式を消して、
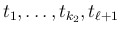 を、
を満たすように取ると、
を、
を満たすように取ると、
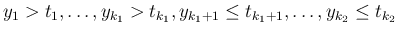
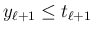 が従う。
よって、(24) の場合、
(22) の左辺からは
が従う。
よって、(24) の場合、
(22) の左辺からは 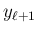 に関する
ものが消える。
に関する
ものが消える。
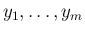 の独立性の仮定から、
その左辺は
の独立性の仮定から、
その左辺は
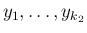 に関する確率の積となり、よって
に関する確率の積となり、よって
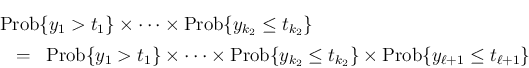
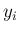 は正規分布に従うのでこれらはいずれも 0 ではなく、
よって
は正規分布に従うのでこれらはいずれも 0 ではなく、
よって
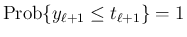
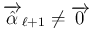 では
起こりえないので矛盾となる。
では
起こりえないので矛盾となる。
結果として、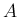 の行ベクトルが線形従属の場合は、
の行ベクトルが線形従属の場合は、
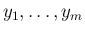 は独立にはならないことが示された。
は独立にはならないことが示された。
竹野茂治@新潟工科大学