![$E[y]=E[\phi(\vec{x})]$](img135.png)
![$E[y]=E[\phi(\vec{x})]$](img135.png) を示す。
まず仮定と結論を明示する。
を示す。
まず仮定と結論を明示する。
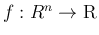 が
が 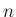 次元密度関数、
次元密度関数、
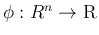 は
は
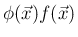 が
が
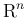 上可積分、すなわち
上可積分、すなわち
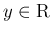 に対し
であるとする。また、
に対し
であるとする。また、
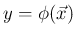 の分布関数
の導関数を
の分布関数
の導関数を 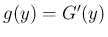 (
(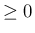 ) とする。
) とする。
このとき、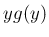 は
は
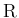 上可積分、すなわち
上可積分、すなわち
証明
正数 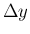 を任意に取る。また、
を任意に取る。また、
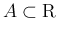 に対して
に対して
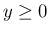 の範囲を
の範囲を  幅の区間
幅の区間
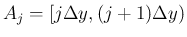 (
(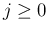 ) に分けると、
) に分けると、
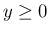 に対して
が成り立つので (両辺は
に対して
が成り立つので (両辺は 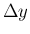 幅の階段関数)、
幅の階段関数)、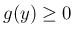 より、
この左辺を
より、
この左辺を 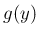 倍して
倍して 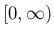 で積分したものを
で積分したものを 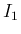 ,
右辺を
,
右辺を 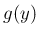 倍して
倍して 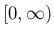 で積分したものを
で積分したものを 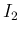 とすると
となる。
とすると
となる。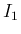 の積分を分けて変形すると、
の積分を分けて変形すると、
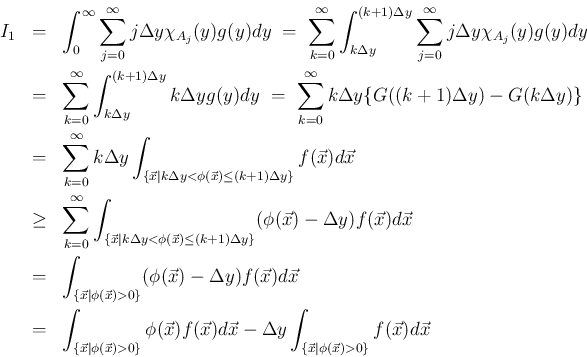
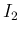 は
は
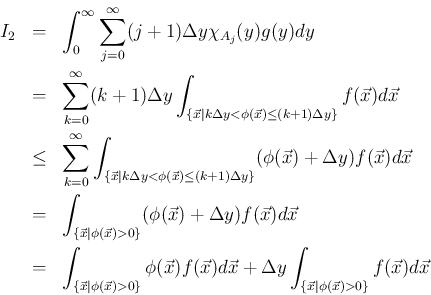
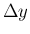 は任意なので、
は任意なので、
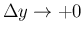 と
すれば (45) より
が得られる。
と
すれば (45) より
が得られる。
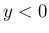 に対しても同様に、
に対しても同様に、
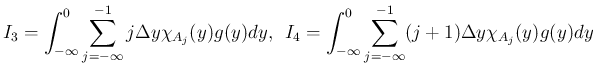

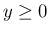 の場合同様、
仮定 (37) と
の場合同様、
仮定 (37) と 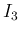 の評価より
が得られ、
の評価より
が得られ、
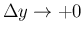 により
が得られる。
により
が得られる。
よって、(46),(50) より (40) が、 (47), (51) より (41) が得られる。
なお、この証明と同じ手法により、任意の
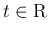 に対して
に対して
竹野茂治@新潟工科大学