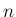
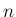 次元球の体積 (9) を
ガンマ関数
次元球の体積 (9) を
ガンマ関数
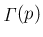 で表すことを考える。
で表すことを考える。
ガンマ関数 (2) は以下のような性質を持つことを 講義で紹介した。
これらについても説明する。
まず、(2) は
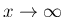 に関して
広義積分であるが、
に関して
広義積分であるが、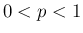 の
の 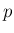 に対しては、
に対しては、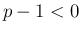 より
より
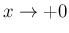 の方も広義積分になっていることに注意する。
の方も広義積分になっていることに注意する。
しかし、
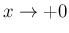 では、
では、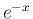 は有界 (
は有界 (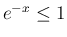 ) で
) で 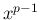 は可積分 (広義積分は収束) なので、
は可積分 (広義積分は収束) なので、
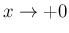 での
広義積分は収束する。
また、
での
広義積分は収束する。
また、
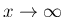 では、
では、
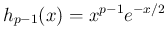 は有界で
は有界で 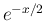 は可積分なので、
は可積分なので、
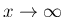 の広義積分も収束する。
なお、
の広義積分も収束する。
なお、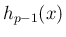 の有界性は、
の有界性は、
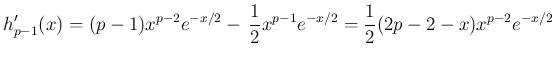
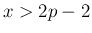 では減少することからわかる。
よって (2) は
では減少することからわかる。
よって (2) は 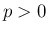 に対して収束する。
に対して収束する。
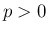 に対し、部分積分により、
に対し、部分積分により、
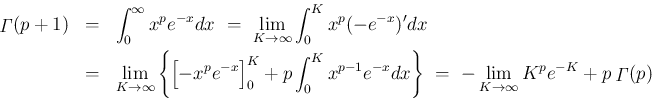
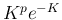 の極限は、
の極限は、
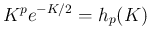 が有界で、
が有界で、
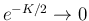 となるから 0 に収束し、
これで (11) の最初のものが得られる。
残りのものは、直接計算して、
となるから 0 に収束し、
これで (11) の最初のものが得られる。
残りのものは、直接計算して、
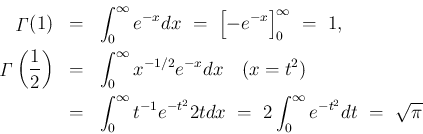
これらを用いると、自然数 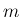 に対し、
に対し、
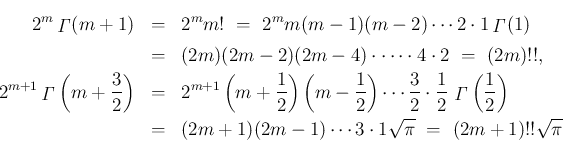
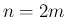 のときは、
のときは、
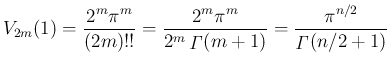
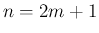 のときは、
のときは、
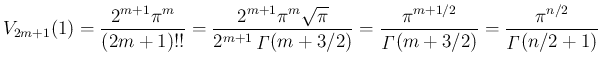
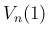 はすべての自然数
はすべての自然数 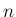 に対して
と書けることになる。
よって、(8) より
に対して
と書けることになる。
よって、(8) より 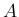 は
は
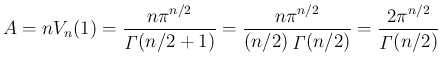
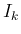 は
と書けることになる。
は
と書けることになる。
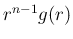 が
が 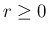 で可積分ならば、
(13) で
で可積分ならば、
(13) で
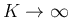 とすれば、
とすれば、
竹野茂治@新潟工科大学