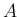 の定義関数を
の定義関数を 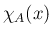 と書く。すなわち、
と書く。すなわち、
以後、実数全体の部分集合 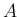 の定義関数を
の定義関数を 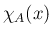 と書く。すなわち、
と書く。すなわち、
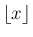 を
を 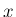 以下の最大の整数、
以下の最大の整数、
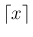 を
を 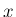 以上の最小の整数
以上の最小の整数
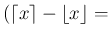 0 または 1) とするとき、
0 または 1) とするとき、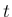 に対し
とすると、
に対し
とすると、
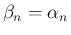 または
または
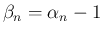 であり、
であり、
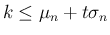 は
は 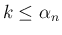 と同値で、
と同値で、
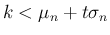 は
は 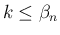 と同値になるので、
と書ける。また、これらの和の
と同値になるので、
と書ける。また、これらの和の 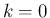 の項を除外して、
の項を除外して、
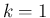 からの和にするが、その場合
からの和にするが、その場合 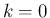 の項は、
の項は、
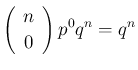
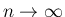 のときに 0 に収束する。
その上で、この和の各項を、区間
のときに 0 に収束する。
その上で、この和の各項を、区間 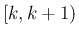 上での
底辺 1 の長方形の面積と考えれば、
丁度ヒストグラムの面積と見ることができて、
上での
底辺 1 の長方形の面積と考えれば、
丁度ヒストグラムの面積と見ることができて、
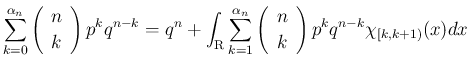
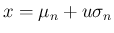 と置換すると、
この式は
と書ける。この被積分関数を
と置換すると、
この式は
と書ける。この被積分関数を 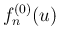 と考える。
と考える。
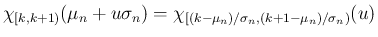
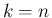 の項
の項 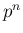 も除外し、
であるから、
も除外し、
であるから、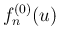 を
を
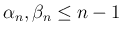 のときに
のときに 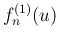 ,
, 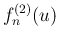 を
を
竹野茂治@新潟工科大学