複素数 ![]() (
(![]() は実数、
は実数、![]() ) に対して、
複素指数
) に対して、
複素指数 ![]() は、オイラーの公式と指数法則を用いて
は、オイラーの公式と指数法則を用いて
また、この ![]() に対し、
に対し、
![]() の範囲の
の範囲の ![]() の
偏角を「偏角の主値」と呼んで、
の
偏角を「偏角の主値」と呼んで、
![]() のように書くことがある。この範囲では偏角は一意的に決まる。
当然、
のように書くことがある。この範囲では偏角は一意的に決まる。
当然、
![]() である。
である。
結局、![]() (不定の
(不定の ![]() は
は ![]() の中に含まれる
と考えることができる) より、
の中に含まれる
と考えることができる) より、
![]() は以下のように定義されることになる。
は以下のように定義されることになる。
ここで、後で使用する偏角に関する性質を、以下にいくつか紹介する。
![]() ,
, ![]() に対して、次が成り立つ。
に対して、次が成り立つ。
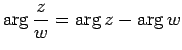
これらは、
![]() ,
, ![]() に対して、
に対して、
また、
![]() は、
は、![]() を使って以下のように表すことができる。
を使って以下のように表すことができる。
![]() (
(![]() ) に対して、
) に対して、
これは、
![]() の定義から容易にわかる。
の定義から容易にわかる。
命題 2 より、
![]() は、
は、
![]() ,
, ![]() の 2 変数関数として各象限で滑らかであり、
(6) より実軸 (
の 2 変数関数として各象限で滑らかであり、
(6) より実軸 (![]() 軸) の
軸) の ![]() の部分でも
滑らかにつながり、(7) より虚軸 (
の部分でも
滑らかにつながり、(7) より虚軸 (![]() 軸) の
軸) の ![]() の部分、
の部分、
![]() の部分でも滑らかにつながっていて、
実軸の
の部分でも滑らかにつながっていて、
実軸の ![]() の部分では不連続になっている:
の部分では不連続になっている:
実数値変数 ![]() の滑らかな複素数値関数
の滑らかな複素数値関数
![]() (
(![]() ) に対して、
) に対して、
![]() は
は ![]() の値が実軸の左側と交わるところで不連続、
それ以外では滑らかな関数となる。
の値が実軸の左側と交わるところで不連続、
それ以外では滑らかな関数となる。
![]() は常に
は常に ![]() の整数倍の不定性を持つことになるが、
逆にそのことを利用して、
の整数倍の不定性を持つことになるが、
逆にそのことを利用して、
![]() の場合に実軸の左側を越えるときに生じる不連続性を
吸収するように不定部分を選ぶことで、
すべての
の場合に実軸の左側を越えるときに生じる不連続性を
吸収するように不定部分を選ぶことで、
すべての ![]() に対して滑らかにできる、と考えることもできる。
しかし、そのようにするには複素関数論の「リーマン面」の理論が
必要になるので、ここでは詳しくは触れない。
に対して滑らかにできる、と考えることもできる。
しかし、そのようにするには複素関数論の「リーマン面」の理論が
必要になるので、ここでは詳しくは触れない。
複素対数の主値
![]() に対して、以下が成り立つ。
に対して、以下が成り立つ。
実数値変数の複素数値関数
![]() (
(![]() ) に対して、
) に対して、
![]() が滑らかな範囲で、
が滑らかな範囲で、
証明
![]() は、
は、![]() の
範囲では (6) より、
の
範囲では (6) より、
よって、その範囲では導関数は、
形式的には、(8) は通常の
実数値関数に対する公式
命題 3 から、 実数変数の複素数値関数の積分公式
竹野茂治@新潟工科大学