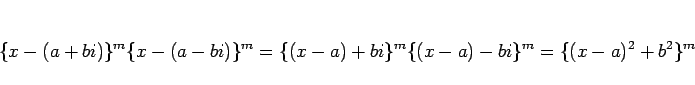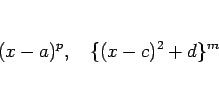を実数係数の範囲でできるだけ因数分解して
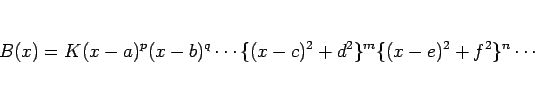
の形 (1 次式と、判別式が負の 2 次式の積) に書くと書かれている ([1], §24 p114)。
これは代数学の基本定理と呼ばれる次の定理から導かれる。
複素数係数の ![]() 次式は、
複素数の範囲で
次式は、
複素数の範囲で ![]() 個の 1 次式の積に因数分解可能である。
個の 1 次式の積に因数分解可能である。
この定理の証明は容易ではなく、さすがにここで行うことはできないが、 この定理と次の事実を用いれば、上に述べた教科書の記述は説明できる。
実数係数の整式が ![]() (
(![]() は実数、
は実数、![]() ,
, ![]() は虚数単位)
という因子を持てば、
その整式は必ず
は虚数単位)
という因子を持てば、
その整式は必ず ![]() という因子も持つ。
という因子も持つ。
複素数 ![]() に対して、
に対して、![]() を
を ![]() の 共役複素数 という。
の 共役複素数 という。
命題 8 の証明
まず、複素数の共役に関して、次を示す。
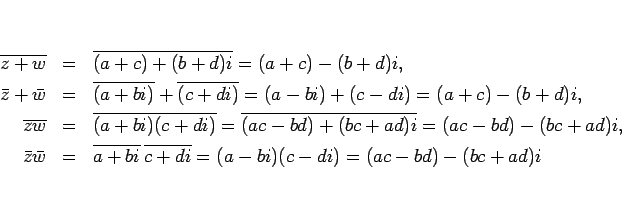
今、整式
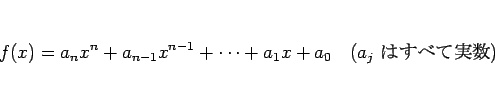
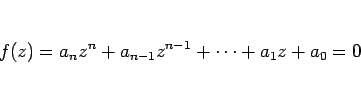
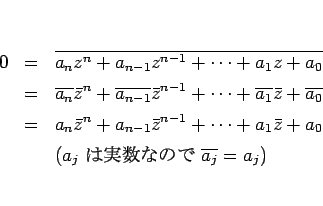
実数係数の整式が
![]() (
(![]() )
という因子を持てば、
その整式は必ず
)
という因子を持てば、
その整式は必ず
![]() という因子も持つ。
という因子も持つ。
証明
実数係数の整式 ![]() が
が
![]() という因子を持つ場合、
命題 8 により少なくとも
という因子を持つ場合、
命題 8 により少なくとも ![]() という因子を持ち、
よって、
という因子を持ち、
よって、![]() は
は
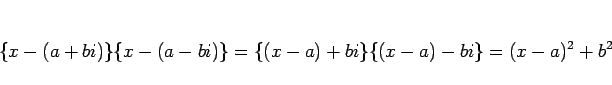
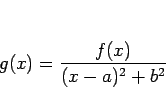
この命題 8 と 系 9 により、
![]() という因子に対しては
という因子に対しては
![]() という因子があり、それをペアで考えれば、
という因子があり、それをペアで考えれば、