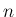
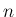 回微分して元に戻る関数を考えてみる。
回微分して元に戻る関数を考えてみる。
これまでの、1 回から 4 回微分して元に戻る関数の結果をまとめると、
以下の通り。
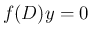 の形に書いて、
その多項式
の形に書いて、
その多項式 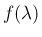 とこれらの解を見比べると、
いくつかの性質が予想される。
とこれらの解を見比べると、
いくつかの性質が予想される。
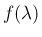 が
が 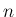 次式ならば
次式ならば 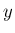 は、
は、
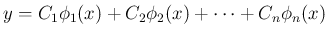
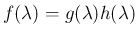 と因数分解され、
と因数分解され、
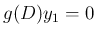 ,
, 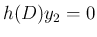 ならば
ならば
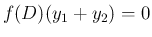 。
。
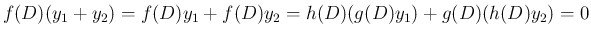
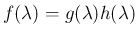 と因数分解される場合、
と因数分解される場合、
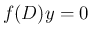 となる任意の
となる任意の 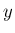 に対し、
に対し、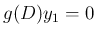 ,
, 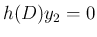 ,
かつ
,
かつ 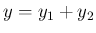 となる
となる 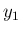 ,
, 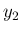 が存在する。
が存在する。
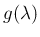 と
と 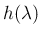 が互いに素、
すなわち定数以外の公約多項式を持たないことが必要であり、
逆に
が互いに素、
すなわち定数以外の公約多項式を持たないことが必要であり、
逆に 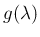 と
と 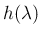 が互いに素であれば 3. は成立する (証明は易しくない)。
が互いに素であれば 3. は成立する (証明は易しくない)。
よって、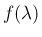 を互いに素なものに因数分解し、
を互いに素なものに因数分解し、
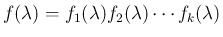
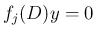 となる
となる 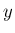 を求めて
を求めて
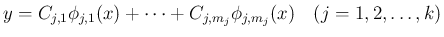
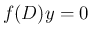 となる
となる 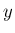 はそれらすべての和
はそれらすべての和
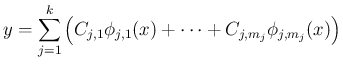
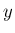 の場合は、
の場合は、
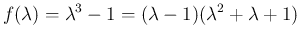
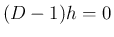 となる
となる 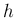 、すなわち (4) と、
、すなわち (4) と、
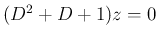 となる
となる 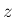 、すなわち (12) を加えた
ものが
、すなわち (12) を加えた
ものが 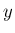 、すなわち (9) の形になる。
だから、3. の事実を使ってよいなら前節までの議論はだいぶ易しくなる (が、
3. 自体の証明は易しくない)。
、すなわち (9) の形になる。
だから、3. の事実を使ってよいなら前節までの議論はだいぶ易しくなる (が、
3. 自体の証明は易しくない)。
(14) から (18) までの方程式の、
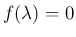 という代数方程式の解を書いてみると、
という代数方程式の解を書いてみると、
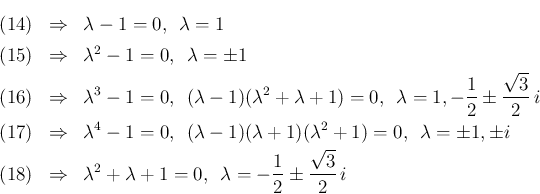
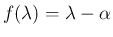 ならば
ならば
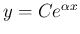
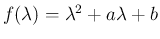 で、
で、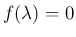 の解が
の解が
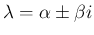 (虚数) ならば、
(虚数) ならば、
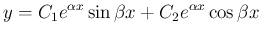
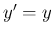 と同じようにして、
5. は (3) から
と同じようにして、
5. は (3) から 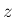 を求めたときと
同じようにすれば示すことができる。
を求めたときと
同じようにすれば示すことができる。
実数係数の 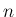 次代数方程式は、代数学の基本定理により、
実数係数の 1 次式か 2 次式のみの積の形に因数分解できることが
知られているので、
次代数方程式は、代数学の基本定理により、
実数係数の 1 次式か 2 次式のみの積の形に因数分解できることが
知られているので、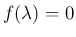 が重解を持たなければ、
これらの性質を組み合わせることで
が重解を持たなければ、
これらの性質を組み合わせることで 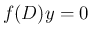 のすべての解が
得られることになる。ただし、重解を持つ場合は少し面倒である。
のすべての解が
得られることになる。ただし、重解を持つ場合は少し面倒である。
さて、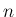 回の微分で元に戻る
回の微分で元に戻る 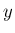 は、
は、
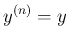
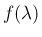 は
は
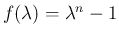 で、
で、
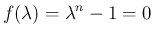
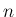 が奇数の場合、(19) のうち
実数解は
が奇数の場合、(19) のうち
実数解は 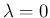 (
(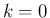 ) のみ、あとはすべて虚数解で、
) のみ、あとはすべて虚数解で、
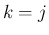 のものと
のものと 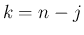 のものが共役な解である (
のものが共役な解である (
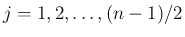 )。
よって、この場合
)。
よって、この場合 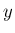 は、4., 5. の線形結合
は、4., 5. の線形結合
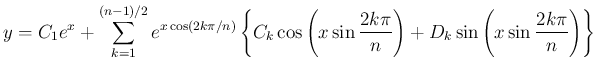
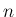 が偶数の場合、(19) のうち
実数解は
が偶数の場合、(19) のうち
実数解は 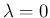 (
(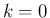 ) と
) と 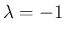 (
(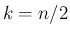 ) の 2 つで、
) の 2 つで、
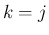 と
と 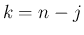 のものが共役な解となる (
のものが共役な解となる (
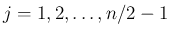 )。
よって、この場合
)。
よって、この場合 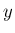 は、
は、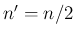 とすれば、
とすれば、
竹野茂治@新潟工科大学