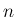
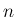 次正方行列
次正方行列 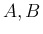 に対し、一般には
に対し、一般には 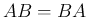 とはならず、
逆に
とはならず、
逆に 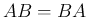 が成り立つとき
が成り立つとき 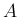 と
と 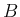 は可換であるという。
は可換であるという。
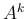 と
と 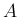 とは、
とは、
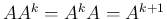 より
より 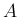 と
と 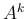 は可換で
あるから、一般に多項式
は可換で
あるから、一般に多項式
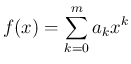 に
対して
に
対して
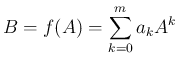 と
と 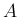 は可換になる。
は可換になる。
本稿では、この逆が成り立つか、すなわち 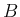 が
が 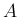 と可換ならば、
なんらかの多項式
と可換ならば、
なんらかの多項式 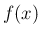 によって
によって 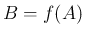 の形に書けるだろうか、
について考えてみる。
の形に書けるだろうか、
について考えてみる。
なお、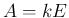 (
(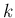 はスカラー、
はスカラー、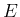 は単位行列) や
は単位行列) や 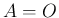 (零行列) の
場合は任意の
(零行列) の
場合は任意の 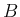 が
が 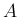 と可換になってしまうので、
本稿では
と可換になってしまうので、
本稿では 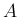 はそのどちらの形でもないと仮定する。
はそのどちらの形でもないと仮定する。
また、ケーリー・ハミルトンの定理により、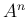 は
は 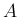 の
の 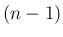 次
以下の多項式で表せるので、
次
以下の多項式で表せるので、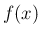 は
は 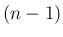 次以下 (
次以下 (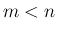 ) の
多項式と考えてよいことに注意する。
) の
多項式と考えてよいことに注意する。
竹野茂治@新潟工科大学