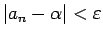ことを意味する。この「限りなく 0 に近づく」とは、どういうことだろうか。が大きくなるとき、
が限りなく 0 に近づく
これは、0 に近づく度合いに限りがない、つまりいくらでも 0 に近づく、 ということを意味しているのであるが、これをいくつかの例で考えてみる。
数列
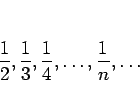
例えば、0.1 (![]() ) よりも近くなるか、
と言えば、それは
) よりも近くなるか、
と言えば、それは ![]() ならば確かに
ならば確かに ![]() なので、
なので、
![]() のときはそうだと言えるだろう。
のときはそうだと言えるだろう。
0.001 (![]() ) よりも近くなるか、と言えば、
それは
) よりも近くなるか、と言えば、
それは ![]() ならば
ならば ![]() なのでそうだと言えるし、
0.00001 (
なのでそうだと言えるし、
0.00001 (![]() ) よりも近くなるか、と言えば、
それは
) よりも近くなるか、と言えば、
それは ![]() ならば
ならば ![]() なのでそうだと言えるだろう。
なのでそうだと言えるだろう。
ここに、「![]() ならば」のような条件がついているが、
極限の説明には「
ならば」のような条件がついているが、
極限の説明には「![]() が大きくなると」と書かれているので、
こういう条件がつくことには問題はない。
つまり、「限りなくいくらでも 0 に近くできる」というのは、
「それに必要なくらい
が大きくなると」と書かれているので、
こういう条件がつくことには問題はない。
つまり、「限りなくいくらでも 0 に近くできる」というのは、
「それに必要なくらい ![]() を大きくしていけば」という条件の下で、
ということを意味しているのだとわかる。
を大きくしていけば」という条件の下で、
ということを意味しているのだとわかる。
よって、0.1 に対して、「![]() ならば
ならば ![]() 」
となるような
」
となるような ![]() を取ることができ、
0.001 に対して、「
を取ることができ、
0.001 に対して、「![]() ならば
ならば
![]() 」
となるような
」
となるような ![]() を取ることができ、
0.00001 に対して、「
を取ることができ、
0.00001 に対して、「![]() ならば
ならば
![]() 」
となるような
」
となるような ![]() を取ることができ、
といったことが、どんな小さな数に対してもいつでもできるようならば、
「
を取ることができ、
といったことが、どんな小さな数に対してもいつでもできるようならば、
「![]() は 0 に収束する」と言う、というのが自然な定義であるように思える。
は 0 に収束する」と言う、というのが自然な定義であるように思える。
これをもう少し明確に述べたのが、次の定義 1 である。
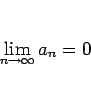
となるようなならば
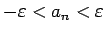
「![]() が
が ![]() に収束する」という場合は、その差
に収束する」という場合は、その差
![]() が
0 に収束すればよく、よって、
が
0 に収束すればよく、よって、![]() ならば
ならば
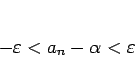
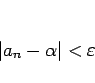
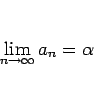
となるようなならば