|
|
(4) |
これも、形式的に次のようにして得られる。
[eatf (t)](s) =
[f (t)](s - a)
(4)
t sin t を t の sin t 倍と見て、 sin t をオイラーの公式により複素指数を使って書き直せばこの公式が使える。 オイラーの公式より、
[eatf (t)](s) =
e-steatf (t)dt =
e-(s-a)tf (t)dt =
[f (t)](s - a)
なので、
eit = cos t + i sin t, e-it = cos t - i sin t
となる。よって、
cos t = , sin t =
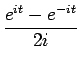
(5)
なので、(5) より
t sin t = t=
teit -
te-it
| = | |||
| = |
| = | 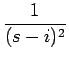 - - 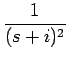 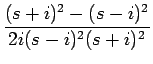 |
||
| = | 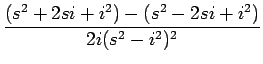 = = 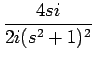 = = 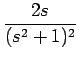 |
なお、この複素指数を利用する方法には、 (6) を利用する以外に、 複素指数倍のラプラス変換の実数部分と虚数部分を考える、 という方法もある。オイラーの公式により、
なので、
[teit] =
[t cos t + it sin t] =
[t cos t] + i
[t sin t]
となるから、1/(s - i)2 を実数部分と虚数部分に分けると、
[teit](s) =
[t](s - i) =
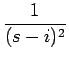
となるので、よって
=
=
=
+ i
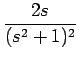
となる、という方法である。 こちらの方が、e-it を使わない分多少楽であるし、 ついでに t cos t のラプラス変換も得られる、というメリットがある。
[t cos t] =
,
[t sin t] =
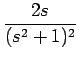
竹野茂治@新潟工科大学