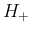
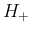 の
の
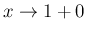 に対する評価を行う。
本節では
に対する評価を行う。
本節では
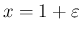 とおいて
とおいて
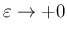 の場合を考える。
の場合を考える。
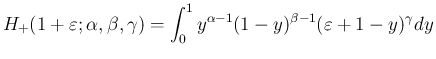
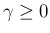 のときは
のときは
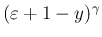 は有界なので、
ルベーグ収束定理により
となる。
は有界なので、
ルベーグ収束定理により
となる。
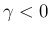 の場合でも、
の場合でも、
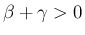 であれば、
であれば、
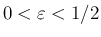 に対して
に対して
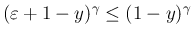 となるので、
ルベーグ収束定理によりやはり (30) が成立する。
よって
となるので、
ルベーグ収束定理によりやはり (30) が成立する。
よって
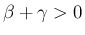 の場合は
の場合は
次は
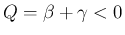 (よって
(よって 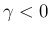 ) の場合を考える。まず、
) の場合を考える。まず、
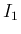 に関しては
に関しては 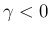 より
より
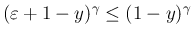 となるので、
となる。
となるので、
となる。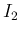 では
では
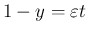 とすると、
とすると、
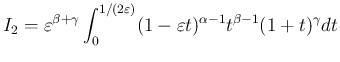
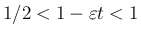 ,
,
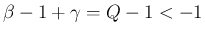 より、
ルベーグ収束定理により
となる。
よって、
より、
ルベーグ収束定理により
となる。
よって、
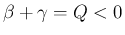 より、
(33), (34) をまとめると、
となることがわかる。この最後の積分は
より、
(33), (34) をまとめると、
となることがわかる。この最後の積分は 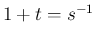 とすれば、
とすれば、
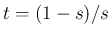 ,
, 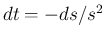 より、
より、
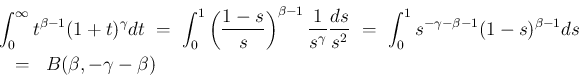
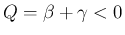 のときは
が言える。
のときは
が言える。
あとは、
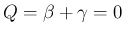 の場合を考えればよい。
の場合を考えればよい。
この場合 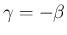 なので、
なので、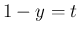 により、
により、
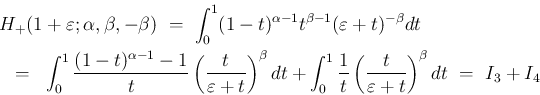
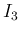 では
では
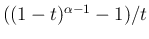 は可積分で、
は可積分で、
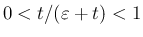 より
となる。以後この極限を
より
となる。以後この極限を 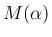 と書くことにする:
なお、本稿では
と書くことにする:
なお、本稿では 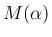 で書き表すが、[1] (p297 2.2.4, 20.) に
よれば、
で書き表すが、[1] (p297 2.2.4, 20.) に
よれば、
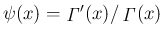 によって
によって
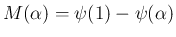
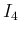 の方は、
の方は、
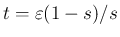 と置換すると、
と置換すると、
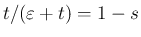 ,
,
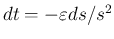 より
より
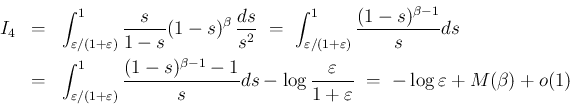
以上をまとめると
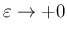 のときに以下が言えることになる。
のときに以下が言えることになる。
これにより、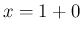 の近くでは、
の近くでは、
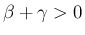 のときは
のときは 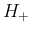 は有界で、
は有界で、
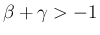 のときは可積分になる。
のときは可積分になる。
竹野茂治@新潟工科大学