これは、 の間違いの問題とは関係ないが、
ついでにきれいな定積分の関係式
の間違いの問題とは関係ないが、
ついでにきれいな定積分の関係式
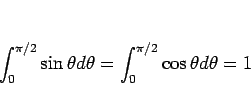 |
(3) |
も図形的に説明できないかと考えた。
これは、
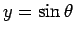 のグラフの下の部分の面積を指している (図 6)。
のグラフの下の部分の面積を指している (図 6)。
図 6:
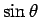 の定積分
の定積分
|
|
式 (3) が成り立つことは、
もちろん不定積分を計算すれば容易にわかるが、
ここでは不定積分を利用せず、それを図形的に説明することを考える。
この面積は、横幅を 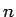 等分して、その分点を
等分して、その分点を 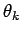 :
:
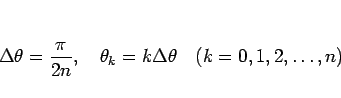
とするとき、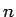 が大きければこの面積は
短冊状の長方形の面積の和で近似できる (区分求積法、図 7):
が大きければこの面積は
短冊状の長方形の面積の和で近似できる (区分求積法、図 7):
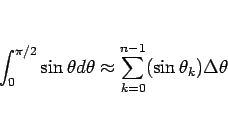 |
(4) |
この、
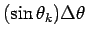 であるが、
図 4 の
であるが、
図 4 の 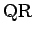 は、
(2) より
は、
(2) より
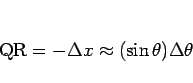
となるので、
図 2 の 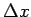 の部分の絶対値である
の部分の絶対値である 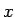 軸上の横幅が、この一つ一つの短冊の面積に相当することになる。
軸上の横幅が、この一つ一つの短冊の面積に相当することになる。
よって、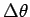 への分割を図 8 のように
円の中心角の分割に置き直して考えれば、
への分割を図 8 のように
円の中心角の分割に置き直して考えれば、
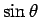 の定積分 (面積) を
の定積分 (面積) を 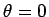 から加えていくのは、
図 8 の各角度に対する
から加えていくのは、
図 8 の各角度に対する 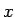 軸上の幅を U から S まで
加えていくことに対応する。
軸上の幅を U から S まで
加えていくことに対応する。
よって、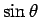 の
の 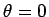 から
から 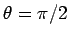 までの積分は、
単位円の
までの積分は、
単位円の 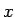 軸の右端の 1 のところから、
軸の右端の 1 のところから、
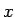 軸の左端の 0 のところまでの横幅を求めることに対応する。
ゆえにその積分は 1 となる。
軸の左端の 0 のところまでの横幅を求めることに対応する。
ゆえにその積分は 1 となる。
同様に、図 4 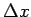 の代わりに
の代わりに 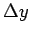 で考えれば、
で考えれば、
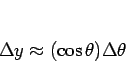
より 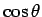 の定積分が
の定積分が 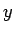 軸上の幅に対応するので、
軸上の幅に対応するので、
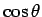 の定積分は図 8 O から T までの幅を
考えていくことに対応し、結局
の定積分は図 8 O から T までの幅を
考えていくことに対応し、結局
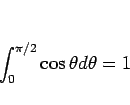
がわかる。
今の議論を、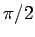 まで伸ばさずに途中で止めて、
まで伸ばさずに途中で止めて、
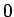 から
から 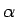 までの定積分を考えれば
よりはっきりするが (図 9)、
これまでの考察より
までの定積分を考えれば
よりはっきりするが (図 9)、
これまでの考察より
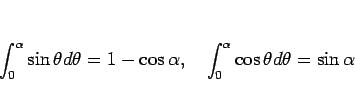
が得られることになる。
さらについでに、図 2 の、
底辺が 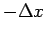 で高さが
で高さが 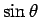 (= Q の
(= Q の 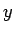 座標) の縦長の長方形の面積を考えれば、
この長方形の面積は
座標) の縦長の長方形の面積を考えれば、
この長方形の面積は
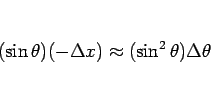
になるので、その和は 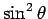 の定積分に相当し、
それはこのような長方形の和である円の一部分の面積に対応する (図 8 の網掛け部分)。よって、
の定積分に相当し、
それはこのような長方形の和である円の一部分の面積に対応する (図 8 の網掛け部分)。よって、
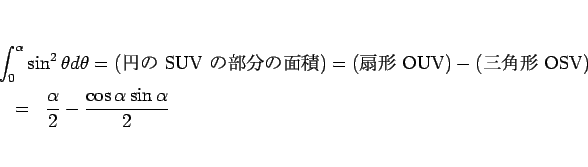
となる。
実際、不定積分を用いて計算すれば、
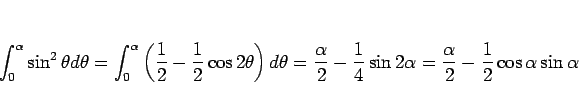
となり、上の結果に等しいことがわかる。
これ以外にも、図形で説明できる同種の定積分が隠れているかもしれない。
竹野茂治@新潟工科大学
2014年7月2日
![]() 等分して、その分点を
等分して、その分点を ![]() :
:
![]() への分割を図 8 のように
円の中心角の分割に置き直して考えれば、
への分割を図 8 のように
円の中心角の分割に置き直して考えれば、
![]() の定積分 (面積) を
の定積分 (面積) を ![]() から加えていくのは、
図 8 の各角度に対する
から加えていくのは、
図 8 の各角度に対する ![]() 軸上の幅を U から S まで
加えていくことに対応する。
軸上の幅を U から S まで
加えていくことに対応する。
![]() の代わりに
の代わりに ![]() で考えれば、
で考えれば、
![]() で高さが
で高さが ![]() (= Q の
(= Q の ![]() 座標) の縦長の長方形の面積を考えれば、
この長方形の面積は
座標) の縦長の長方形の面積を考えれば、
この長方形の面積は