gnuplot-6.0.0 から関数ブロック (function blocks) が使用できるようになりました。 これは、gnuplolt スクリプト内部で関数を定義して利用できる機能で、 従来の関数定義は 1 本の数式でしか関数は定義できませんでしたが、 関数ブロックでは、より複雑な式を使ったサブルーチン形式で関数を定義でき、 局所変数や、gnuplot の set コマンドなども使用することが可能です。
また、この関数ブロックは、値を返す関数だけでなく、 いくつかの gnuplot コマンドを引数に応じて実行する「子スクリプト」 のような使い方も可能で、その場合は evaluate で実行します。
ただし、関数の実行速度は早くないですし、 関数ブロック内で関数ブロックを使用したり、 plot や stats コマンド等を再帰的に使用、 すなわち plot コマンドで呼び出す関数ブロック内部で plot や stats を使用することはできません。
ここでは関数ブロックの使用例として、 ルーローの三角形の回転アニメーションを紹介します。 ルーローの三角形自体は set object で描画しますが、 それを関数ブロックを用いてサブルーチン化します。 ルーローの三角形は、正三角形の回りに円弧を追加することで 「等幅曲線」にしたものです。
正三角形の一辺が r で、中心が px,py のルーローの三角形を rot 度だけ回転したものは以下のように関数ブロック化できます。
function $reuleux(r,px,py,rot) << EOD
local rr = r/sqrt(3)
local pr = 0.02*r
local rrot = rot*pi/180
local p1x = px + rr*cos(rrot)
local p1y = py + rr*sin(rrot)
local p2x = px + rr*cos(rrot + 2*pi/3)
local p2y = py + rr*sin(rrot + 2*pi/3)
local p3x = px + rr*cos(rrot + 4*pi/3)
local p3y = py + rr*sin(rrot + 4*pi/3)
unset for [i=1:5] object i
set object 1 circle at px,py size pr lt 1 fs solid
set object 2 polygon from p1x,p1y to p2x,p2y to p3x,p3y
to p1x,p1y lt 1 lw 2
set object 3 circle at p1x,p1y size r
arc [rot+150:rot+210] lt 1 lw 2
set object 4 circle at p2x,p2y size r
arc [rot+270:rot+330] lt 1 lw 2
set object 5 circle at p3x,p3y size r
arc [rot+30:rot+90] lt 1 lw 2
EOD
見てわかるように、全体の構造はデータブロックと同様に ヒアドキュメント形式になっています。 関数ブロックの引数、ここでは r, px, py, rot は関数ブロック内部のみで利用可能 (スコープ) な局所変数で、 さらに内部でも local をつけて定義した局所変数を利用できます。
rr は中心から各頂点までの距離、pr は 中心に置く点の半径、 rrot は rot をラジアンに変換したもの、 (p1x,p1y),(p2x,p2y),(p3x,p3y) は正三角形の頂点です。 正三角形は set object polygon で、 追加の円弧は set object circle で描画しています。 unset object で一度前の object を消去してから 新たに描画するようにしています。
なお、これを正しくルーローの三角形として描画するには、 x 軸と y 軸の縮尺が 1:1 でないといけませんので、 「set size ratio -1.0」が必要です。
これは、値を返さない関数 (手続き) なので、 evaluate で呼び出します。 以下のようにすれば、 ルーローの三角形のころがるアニメーションが見られます。
a = 6
set xrange [-a*pi/6:a*pi/2]
set yrange [0:a]
set size ratio -1.0
set xtics format "%.1Ppi"
set xtics -a*pi/2, a*pi/6
set ytics a/3.0
set grid
pi180 = pi/180
ar = a/sqrt(3)
do for [rot=0:60:1] {
cx = a*rot*pi180 + ar*sin((30 - rot)*pi180)
cy = a - ar*cos((30 - rot)*pi180)
evaluate $reuleux(a,cx,cy,-rot)
plot 0 not
pause 0.01
}
ころがると円弧の弧長分だけ右に進み (a*rot*pi180)、 正三角形の上の頂点が常にその接地点の距離 a だけ真上にあり、 中心はその上の頂点から距離 ar、角度は鉛直下向き方向から 30-rot 度回転したところにあります。 最後に set object の図を描画するために plot 0 を実行しています。
これで 60 度回転する分が表示されますが、 接地点を固定したまま 60 度回転するとまたスタートと同じ形になり、 それを繰替えせば、ころがり続けるルーローの三角形ができます。
a = 6
set xrange [-a*pi/6:a*4*pi/3]
set yrange [0:a]
set size ratio -1.0
set xtics format "%.1Ppi"
set xtics -a*pi/2, a*pi/6
set ytics a/3.0
set grid
pi180 = pi/180
ar = a/sqrt(3)
do for [j=0:2] {
do for [rot=0:60:1] {
cx = a*(rot+60*j)*pi180
+ ar*sin((30 - rot)*pi180)
cy = a - ar*cos((30 - rot)*pi180)
evaluate $reuleux(a,cx,cy,-rot)
plot 0 not
pause 0.01
}
do for [rot=0:60:1] {
cx = a*(j+1)*60*pi180
+ ar*cos((120 - rot)*pi180)
cy = ar*sin((120 - rot)*pi180)
evaluate $reuleux(a,cx,cy,-60-rot)
plot 0 not
pause 0.01
}
}
- ルーローの三角形車輪のころがり動画 :webp terminal 出力
(画像クリックすると動画再生)
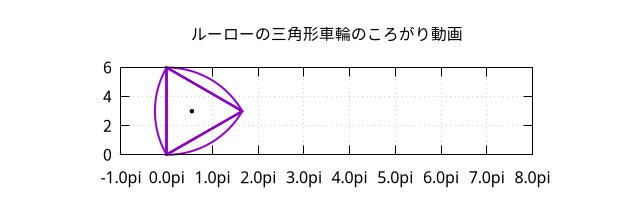
- ルーローの三角形車輪のころがり動画 :
pngcairo terminal 出力を animation gif にしたもの
(画像クリックすると動画再生)
中心が上下に移動しながら進むことがわかると思います。
なお、この中心は、常に接地点の真上にあるわけでもなく、
接地点より前に出たり、後ろに下ったりもしています。
円弧部分が接地している場合は接地点の真上にあるのはむしろ上の頂点になります。
上のスクリプトの cx の先頭の項の a*(rot+60*j)*pi180 や
a*(j+1)*60*pi180 は、
接地点の初期位置からの移動距離を表しますので、
それを削除すると、接地点を固定した状態での
ルーローの三角形のころがりの様子が見れます。
これを見ると、中心がどのように動くかむしろわかりやすいかと思います。
- 接地点を固定したころがり動画: webp teminal 出力
(画像クリックすると動画再生)
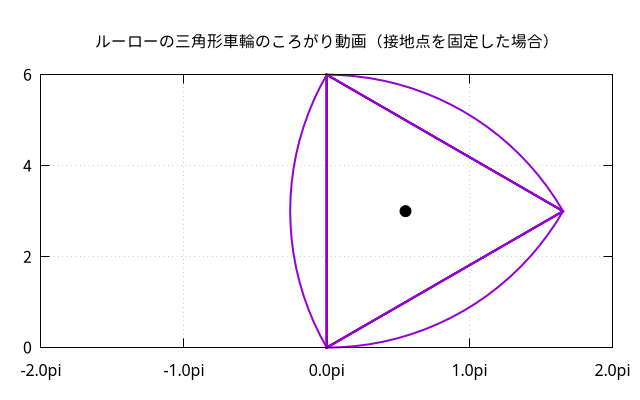
- 接地点を固定したころがり動画:
pngcairo terminal 出力を animation gif にしたもの
(画像クリックすると動画再生)
なお、今回はアニメーション画像として、webp terminal 出力のものと、 pngcairo terminal 出力の PNG ファイルを GIF に変換して animation gif にまとめたものを用意しましたが、 webp 出力の方は gnuplot のみで完結するので、こちらの方がずっと楽です。 ただし、delay (フレーム間隔) が webp の方が開くのか、 それともブラウザ処理が遅いのか、 うちの環境では webp 出力の方が遅く表示されます。
今回用いた function block によるサブルーチン化は、従来の gnuplot でも 子スクリプトを使うなどの方法で実現できなくはありませんが、 function block の方が保守やテストも楽ですし、 プログラムを書き慣れている人には便利な仕組みだと思います。
「情報やメモ (09/06 2023)」 で報告した、spiderplot で title columnheader を使うと空行の key が生成されてしまう問題ですが、gnuplot-6.0 でも残っていますが (少なくとも 6.0.2 までは)、 一応 04/09 の git 版から解消されました。
なお、spiderplot (や parallelaxes) の「軸」やデータの扱い、 そして key や title の扱いは、 他の描画スタイルとかなり違うので注意が必要です。
通常の描画スタイルでは、plot では軸は 2 軸でデータは (x,y) となっていて、2 軸の張る 2 次元平面上に点 (x,y) のグラフを描くわけですが、 spiderplot や parallelaxes では「軸」は複数あり、 データは各「軸」毎に 1 つずつの列データを指定し、 そのデータの点をその「軸」上に 1 次元的に描画し、 複数回の plot コマンドで複数の軸のデータを与えてそれを線で結ぶ、 という方法になっています。
つまり、with line の場合は、データが
x1 y1 z1のときに「
x2 y2 z2
x3 y3 z3
plot "data" using 1:2, '' using 1:3」
とすれば、一つ目の plot で (x1,y1) の点, (x2,y2) の点,
(x3,y3) の点を順に線分で結び、
2 つ目の plot で (x1,z1) の点, (x2,z2) の点, (x3,z3) の点を
順に線分で結んでいくのですが、
spiderplot, parallelaxes の場合は、
x1 x2 x3のデータ (上のデータの転置) に対して、 「
y1 y2 y3
z1 z2 z3
plot "data" using 1, '' using 2, '' using 3」
とすると軸 1 上の x1, 軸 2 上の x2, 軸 3 上の x3 の点を順に線分で結び、
次に 軸 1 上の y1, 軸 2 上の y2, 軸 3 上の y3 の点を順に線分で結び、
次に 軸 1 上の z1, 軸 2 上の z2, 軸 3 上の z3 の点を順に線分で結ぶ、
という形を取ります。
つまり、「線分で結ぶ一つのグラフ」という単位が、 with line ではデータの縦並び (列) であるのに対して、 spiderplot や parallelaxes ではデータの横並び (行) になります。 そのため、通常の plot では各 plot 要素毎 (＝グラフの単位) につける「title」 でグラフの単位毎に key を生成していますが、 spiderplot や parallelaxes では各 plot 要素がグラフの単位ではなく、 「軸」の単位となってしまうため、 plot 要素に「title」をつけても、 それが key を生成したらおかしなことになってしまいます。
そこで、spiderplot や parallelaxes では、 その plot 要素毎の「title」(＝「軸」の単位) を、 key ではなく、例外的に「軸」のラベルとして使うようになっていて、 よって columnheader() を使用すれば データの先頭列の文字列を「軸」の名前として貼ることができ、 逆に key には何も生成されません。
ただ、この title による軸ラベルの生成は、 少なくとも spiderplot ではあまりオフィシャルなものではないようで、 実際開発者は、spiderplot では title は無効なもので、 「key()」や「keyentry」を使って key を生成し、 軸ラベルは「set paxis label」を使うべき、と考えているようです。 spiderplot に関するドキュメントにもほぼそのように書かれていて、 title を使用する例は書かれていませんが、 set paxis の項目のところに「平行座標描画 (parallelaxes) の軸は、 plot コマンドの `title` オプションでラベル付けできます」 と書かれていて、これが spiderplot でもほぼ有効になっているのが 上、そして 「情報やメモ (09/06 2023)」 の [b-1] の title columnheader の利用につながっているわけです。
gnuplot の歴史みたいなものを一度まとめておこうかなと思い、 そのために古い gnuplot を少し調べてみました。
今まで、gnuplot-2.0 や gnuplot-1.10A というものがあることは知っていたのですが、 それより前のものは知りませんでいた。 今回、gnuplot の SourceForge を調べてみたら、Git Repository に gnuplot-1.1 (1.1.0) があることを知りました。1.10A より前のものです。 正確には、version.c を見ると、1.10A は 1.1.0A (1989-03-18) で、 1.1 は 1.1.0 (1987-01-26) です。 Git Repository にあるのはこれが一番古いもののようです。
しかし、gnuplot の本家のページ http://www.gnuplot.info には、「Release History」のところに 「gnuplot 1.0 1986」と書かれていますので、 1.0 もどこかにあるはず、と探してみたらありました。
昔まだ Web が発達していないころは、フリーソフトの多くは、 anonymous ftp サイトで配布されていたり、 あるいはネットニュース (Usenet) でテキスト形式に変換した形で 配布されていたりしていました。 gnuplot も同様で、1.10A や 2.0, 3.0 などは Usenet の comp.sources.misc で配布されていました。 その前の方を辿ると、comp.sources.misc の前身のような net.sources にありました。 現在でも、Usenet のアーカイブをしているサイトがいくつかあり、 そこで取得することができます。
- Usenet アーカイブサイト :
https://www.usenetarchives.com/
- その comp.sources.misc : Usenet Archives COMP.SOURCES.MISC
- その net.sources : Usenet Archives NET.SOURCES
- Usenet アーカイブサイト :
https://usenet.trashworldnews.com/
- その comp.sources.misc : [..] comp.sources.misc
- その net.sources : [..] net.sources
前者のサイトのものは、なぜかソースの一部分 (ソース各行の < より後ろの部分) が欠けてしまっているので、 完全なソースは復元できません。 後者のサイトのものなら OK のようです。 gnuplot-1.0 は以下に 4 分割して投稿されていて、 アナウンスも入れると 5 回の投稿です。 それが一つにまとまっています。
- GNUPLOT (5 replies, 11/24/86) : https://usenet.trashworldnews.com/?thread=114748
11/24 と書かれていますが、実際の投稿は 1986-11-18 です。 これらは、自己解凍形式のシェルスクリプトで投稿されたもので、 必要な部分を切り出して sh を実行すればソースが展開されます。 ソースをまとめ直したものも以下に置いておきます。
- gnuplot-1.0.tar.Z (121043 Byte)
version.c を見ると、バージョンは 1.0.3 (1986-11-16) となっています。 ということは、これより前の 1.0.0 もあるのでしょうが、 多分広く公開された最初のバージョンがこの 1.0.3 なのではないかと思います。 付属の README を見ると、
GNUPLOT has been tested on a Pyramid 90x (ucb 4.2 and att V), a VAX 8200 (VMS 4.3), IBM PC's and AT's (MS-DOS 3.1, Microsoft C 4.0).とあります (アナウンスにも同様に書かれています) から、 なんと最初から Unix と VMS, MS-DOS (PC) のマルチプラットフォームでの動作を意識していたことがわかります。 ただ、かなり古いソースなので、そのままコンパイルすることは難しいでしょう。 Makefile のスペースをタブに変換しないといけない箇所もあります。 むしろソースやドキュメントが色々参考になりそうです。
最新の開発版 (git) の all.dem の出力を置いておきます。
- all.dem の PDF 出力 (2025-02-25 の GIT 版)
all-current-20250225.pdf (786 ページ、26,771,273 Byte) - その画像を小さくした一覧 (2025-02-25 の GIT 版)
all-20250225-list.pdf (14 ページ、35,026,975 Byte)
「情報やメモ (12/03 2024)」 の時点のデモ (782) と比べると、以下が変更されています。
- 変更: 683 ページのものが 514 ページへ移動 (extra_points.dem)
- 新規追加: 515-518 ページ (mark_formulas.dem, mark_grouping.dem, mark_labels.dem, windbarb.dem)
この新規追加の 4 つのデモは、いずれも新しく追加された with marks のデモです。with marks は、 「情報やメモ (08/23 2024)」 の時点で既に GIT 版に追加されていますが、 その後ドキュメントやデモが今回追加されています。
「情報やメモ (12/03 2024)」 からの改変には、以下のようなものがありますが、抜けもだいぶあると思います。
- with marks, set mark, set object mark の説明と例がマニュアルに追加
- watchpoint のラベルとして、文字列値関数を指定することもできるように
- save コマンドに marks の設定を保持する save marks が追加
このマーク機能により、自分でも記号を容易に定義できるので、 グラフ上に打てる記号のバリエーションがほぼ無限に広がります。 実際、上のデモの 518 ページは、 天気図の風向風力記号をマーク機能で表現したものです。
さらに、このマーク機能を応用して「グラフに注釈をつける」ことにも使えます。 それが、上のデモの 516-517 ページのデモです。 棒グラフの上についているグループを示す注釈、 および積み上げ型のヒストグラムの右についている線と文字列の注釈が マークを応用してつけられています。
これまでの gnuplot でも、set arrow や set label を駆使すれば、 注釈機能を実現することは不可能ではありませんでしたが、 かなり不自然ですし、スクリプトが相当長くなってしまいます。 それがこのマーク機能では かなり自然なわかりやすい形で実現されていると思います。 まだ私もそれほど把握できていませんので、 今後徐々に使ってみたいと思います。