4.6 接触不連続
4.5 節の最後の
(4.35) より、
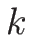 -特性方向が真性非線形であれば
-特性方向が真性非線形であれば 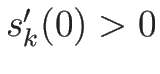 なので、
少なくとも
なので、
少なくとも 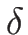 が 0 の近くであれば
曲線
が 0 の近くであれば
曲線 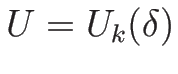 に沿って
に沿って
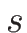 も変化することがわかるが、
も変化することがわかるが、
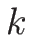 -特性方向が線形退化の場合には
-特性方向が線形退化の場合には 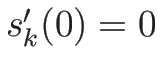 となりあまり変化がない。
これが実際に全く変化しないことをこの節で紹介する。
となりあまり変化がない。
これが実際に全く変化しないことをこの節で紹介する。
まず、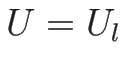 を通り、ベクトル場
を通り、ベクトル場 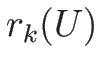 に対する
に対する
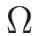 内の積分曲線
内の積分曲線 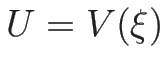 を取る:
を取る:
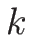 -特性方向が線形退化の場合は、
この積分曲線が
-特性方向が線形退化の場合は、
この積分曲線が 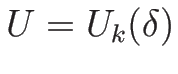 の作る曲線であることを示す。
の作る曲線であることを示す。
より、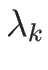 はこの積分曲線に沿って定数、すなわち、
はこの積分曲線に沿って定数、すなわち、
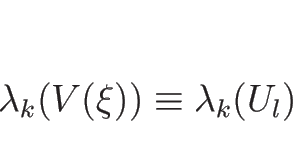 |
(4.85) |
であることがわかり、また、(4.36) より、
となるので、
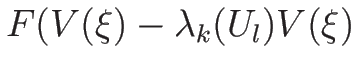 も定数、すなわち
も定数、すなわち
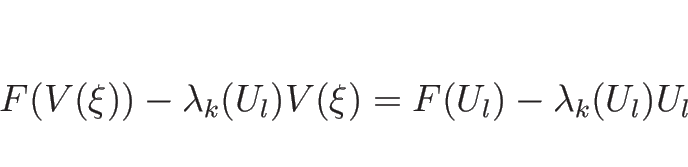 |
(4.86) |
が成り立つ。
これは、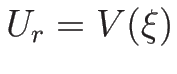 ,
,
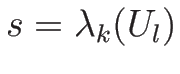 に対する
ランキン-ユゴニオ条件を意味している。
この (4.37) と
(4.27), (4.28) の
関係を見るために、(4.37) を
少し変形する。
に対する
ランキン-ユゴニオ条件を意味している。
この (4.37) と
(4.27), (4.28) の
関係を見るために、(4.37) を
少し変形する。
なので、
となり、よって、ある 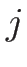 に対し、
に対し、
となることがわかる。
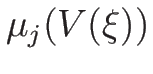 は連続で
は連続で
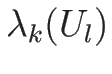 は一定なので、
は一定なので、
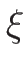 毎に
毎に 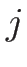 は変化したりはせず、
は変化したりはせず、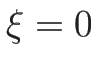 では
では
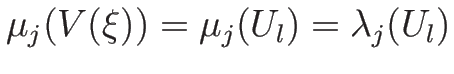 なので
なので
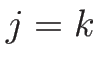 でなければならない。
でなければならない。
よって、あるスカラー関数 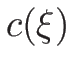 によって
によって
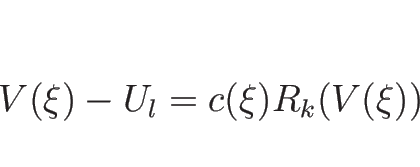 |
(4.87) |
となることになる。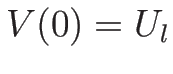 であるから
であるから 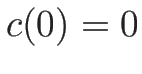 で、
(4.38) を
で、
(4.38) を 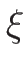 で微分して
で微分して 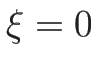 とすれば、
とすれば、
となるので、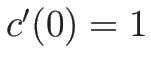 、よって
、よって 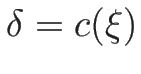 は
は 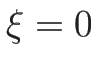 の近くで
逆関数
の近くで
逆関数
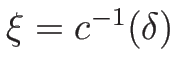 を持つので、
(4.38) と
(4.28) を比較すれば、
を持つので、
(4.38) と
(4.28) を比較すれば、
となることがわかる。
結局、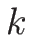 -特性方向が線形退化の場合は、
-特性方向が線形退化の場合は、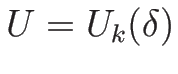 ,
,
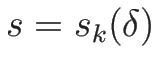 は、
は、
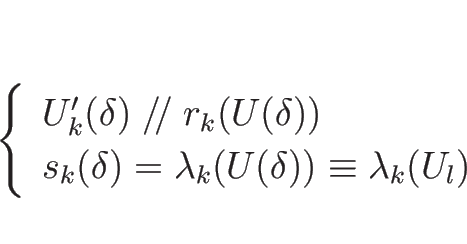 |
(4.88) |
を満たし、よって 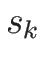 は
は 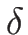 に関して定数、
に関して定数、
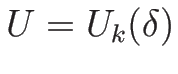 は相空間上で
は相空間上で 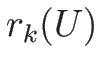 の積分曲線を動くことになる。
の積分曲線を動くことになる。
これによる不連続解を、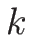 -接触不連続 (
-接触不連続 (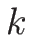 -contact discontinuity) と呼ぶ。
不連続線の方向は、左右の
-contact discontinuity) と呼ぶ。
不連続線の方向は、左右の 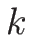 -特性曲線の方向 (
-特性曲線の方向 (
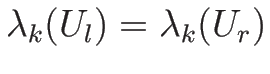 )
と一致する。
)
と一致する。
図 4.4:
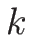 -接触不連続解 (点線は
-接触不連続解 (点線は 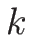 -特性曲線)
-特性曲線)
|
|
竹野茂治@新潟工科大学
2018-08-01
![]() を通り、ベクトル場
を通り、ベクトル場 ![]() に対する
に対する
![]() 内の積分曲線
内の積分曲線 ![]() を取る:
を取る:
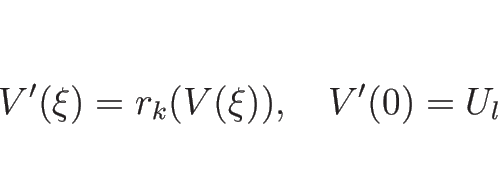
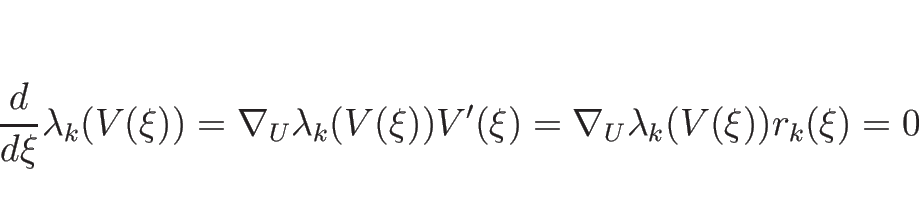
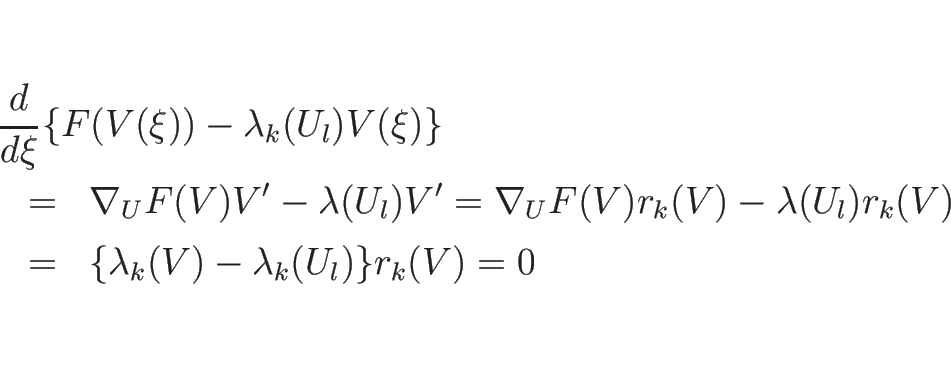
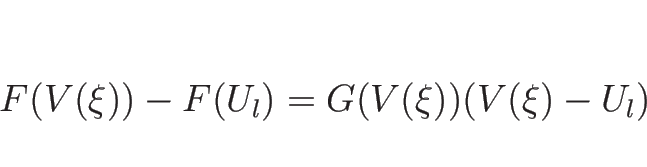
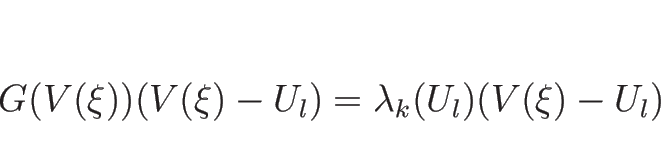
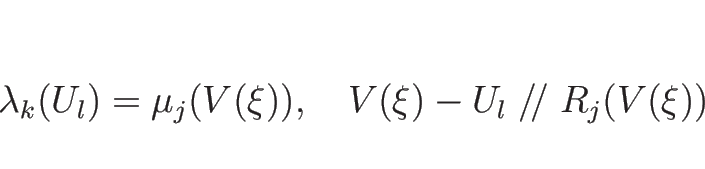
![]() によって
によって
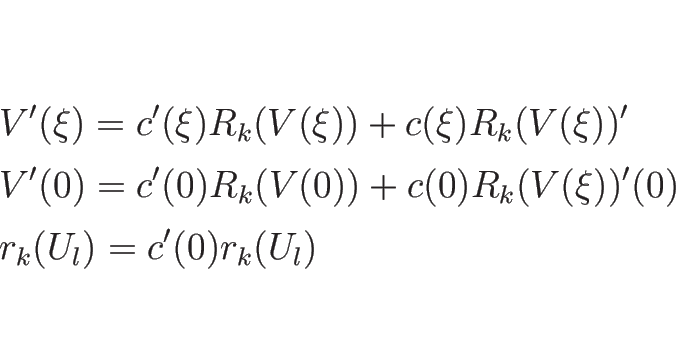
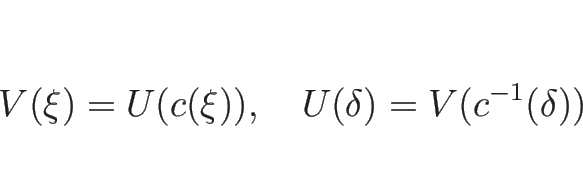
![]() -特性方向が線形退化の場合は、
-特性方向が線形退化の場合は、![]() ,
,
![]() は、
は、
![]() -接触不連続 (
-接触不連続 (![]() -contact discontinuity) と呼ぶ。
不連続線の方向は、左右の
-contact discontinuity) と呼ぶ。
不連続線の方向は、左右の ![]() -特性曲線の方向 (
-特性曲線の方向 (
![]() )
と一致する。
)
と一致する。