また、[2] では、0 から ![]() までの定積分であったが、
今回の (15) は 0 から
までの定積分であったが、
今回の (15) は 0 から ![]() までの定積分、
つまり実質的に不定積分の計算なので、
積分範囲は外して、不定積分の変数変換の計算のみを行う。
ただし、厳密には、
までの定積分、
つまり実質的に不定積分の計算なので、
積分範囲は外して、不定積分の変数変換の計算のみを行う。
ただし、厳密には、![]() の範囲によっては 0 から
の範囲によっては 0 から ![]() までの積分を 2 つ、
4 つなどと分けないといけないのであるが、
そういう話もほぼ省略する (一つだけ紹介する)。
までの積分を 2 つ、
4 つなどと分けないといけないのであるが、
そういう話もほぼ省略する (一つだけ紹介する)。
(15) で、![]() ,
, ![]() とし、
それを不定積分の形に書いたものを
とし、
それを不定積分の形に書いたものを ![]() とすると
とすると
(16)
しかし、本来は
![]() なので、
なので、![]() とす場合は、
とす場合は、
![]() の場合と
の場合と
![]() の場合に分けて考え、
後者の場合は積分を 0 から
の場合に分けて考え、
後者の場合は積分を 0 から ![]() までの積分と
までの積分と ![]() から
から ![]() までの積分の 2 つに分けた上で置換する必要がある。
これが、この節の冒頭に書いた「厳密には積分を分けて考えないといけない」
という話である。
ただ、分けた積分でもほぼ同じ置換を行うので、
不定積分の計算では本質的には分けて考える必要はない。
までの積分の 2 つに分けた上で置換する必要がある。
これが、この節の冒頭に書いた「厳密には積分を分けて考えないといけない」
という話である。
ただ、分けた積分でもほぼ同じ置換を行うので、
不定積分の計算では本質的には分けて考える必要はない。
さらに、
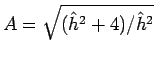 とした上で
とした上で ![]() と置換すると、
と置換すると、
![]() より、
より、
この被積分関数は、
![]() とすると、
とすると、
以上により、![]() が楕円積分に帰着されることがわかり、
(15) は一般には初等関数で
表すことはできないことがわかる。
が楕円積分に帰着されることがわかり、
(15) は一般には初等関数で
表すことはできないことがわかる。
竹野茂治@新潟工科大学