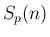
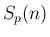 は次の性質を持つことが知られていて、
それをファウルハーバーの定理と呼ぶようである。
は次の性質を持つことが知られていて、
それをファウルハーバーの定理と呼ぶようである。
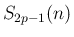 は
は 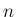 の多項式として
の多項式として 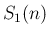 で割り切れ、
さらにその商は
で割り切れ、
さらにその商は 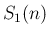 の多項式で表される (
の多項式で表される (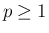 )。
)。
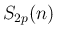 は
は 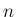 の多項式として
の多項式として 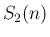 で割り切れ、
さらにその商は
で割り切れ、
さらにその商は 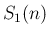 の多項式で表される (
の多項式で表される (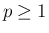 )。
)。
(17) より、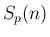 に対する性質 [T1], [T2] は、
に対する性質 [T1], [T2] は、
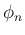 に対する次の性質 [T1'], [T2'] に書き直すことができる。
に対する次の性質 [T1'], [T2'] に書き直すことができる。
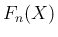 により
により
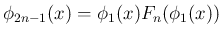 となる (
となる (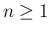 )。
)。
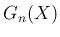 により
により
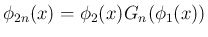 となる (
となる (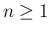 )。
)。
この性質 [T1'], [T2'] を、漸化式 (15) を用いて 直接示すこともできるが、本節では、この [T1'], [T2'] が、 さらに少し変形した形 [S1], [S2] と同等であることを示し、 そちらを証明することで [T1], [T2] が成り立つことを示すことにする。
そのために、
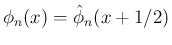 , すなわち
, すなわち
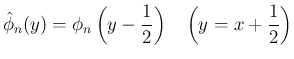
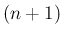 次多項式
次多項式
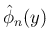 を導入すると、
[T1'], [T2'] は次の形に書ける (
を導入すると、
[T1'], [T2'] は次の形に書ける (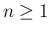 )。
)。
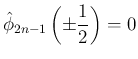 で、
かつ
で、
かつ
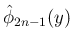 は偶関数 (偶数次の項のみの多項式)
は偶関数 (偶数次の項のみの多項式)
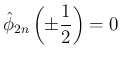 で、
かつ
で、
かつ
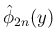 は奇関数 (奇数次の項のみの多項式)
は奇関数 (奇数次の項のみの多項式)
この、[T1'],[T2'] と [S1],[S2] が同等であることを示そう。
まず、[T1'] が成り立てば、
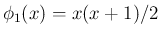 より、
より、
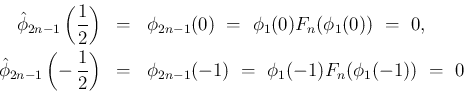
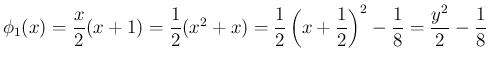
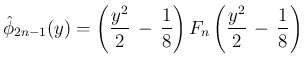
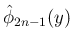 は偶関数となり、
よって [S1] が得られる。
は偶関数となり、
よって [S1] が得られる。
同様に [T2'] が成り立てば、
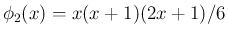 より、
より、
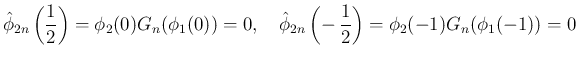
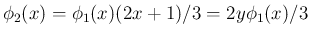 より、
[T2'] から
より、
[T2'] から
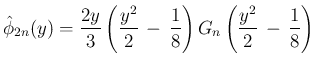
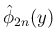 は奇関数となり、
よって [S2] が得られる。
は奇関数となり、
よって [S2] が得られる。
逆に、[S1] が成り立てば、
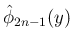 は
因数定理により
は
因数定理により
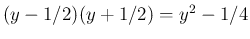 で割り切れるので、
その商を
で割り切れるので、
その商を 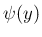 と書けば
と書けば
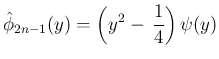
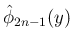 は偶関数なので、
は偶関数なので、
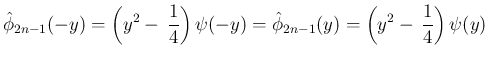
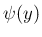 も偶関数の多項式で、
よって
も偶関数の多項式で、
よって
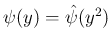 の形に書ける (
の形に書ける (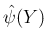 も多項式)。よって
も多項式)。よって
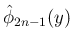 は
は
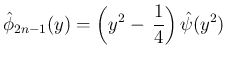
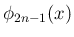 に戻せば、
に戻せば、
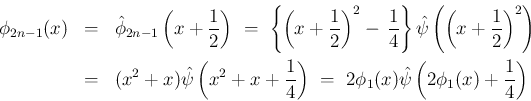
同様に、[S2] が成り立つならば、
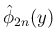 は、
ある多項式により
は、
ある多項式により
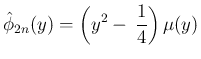
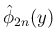 は奇関数なので、
は奇関数なので、
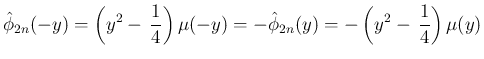
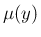 も奇関数の多項式で、
特に
も奇関数の多項式で、
特に 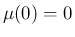 であるから
であるから 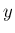 で割り切れ、その商は偶関数となる。
よって、
で割り切れ、その商は偶関数となる。
よって、
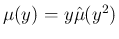 (
(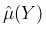 も多項式) の
形になるので、
も多項式) の
形になるので、
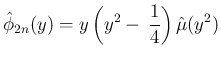
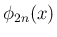 に戻せば、
に戻せば、
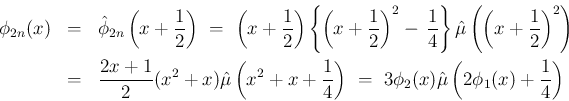
よって、あとは [S1],[S2] が成り立つことを示せばよいのであるが、
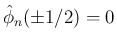 は、
は、
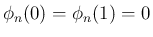 と同等で、
それは漸化式 (15) から、
成り立つことが帰納的に容易に示される ((15) に
と同等で、
それは漸化式 (15) から、
成り立つことが帰納的に容易に示される ((15) に 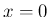 ,
, 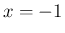 を代入すればいずれも 0 になる) ので、
あとは偶関数、奇関数の部分のみ考えればよい。
を代入すればいずれも 0 になる) ので、
あとは偶関数、奇関数の部分のみ考えればよい。
今、関数 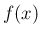 から、新たな関数を作る変換演算子
から、新たな関数を作る変換演算子 ![$T[f]=T[f](x)$](img126.png) を、
を、
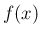 ,
, 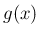 と
定数
と
定数 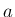 ,
, 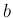 に対して
に対して
 = aT[f](x)+bT[g](x)
$](img132.png)
さて、あと [S1],[S2] で示すべきは、
「であるが、これは、が偶関数で、
が奇関数であること」
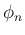 で言えば
で言えば
「を意味する。よってこれを示すためには、(20) とが
の偶数次の項からなる多項式、
が
の奇数次の項からなる多項式となること」
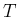 の
線形性により、
の
線形性により、
「を示せばよい。あとはこれを実際に計算で示す。の偶数乗 (0 乗以上) の
による変換結果が
の奇数次の項のみで表され、
の奇数乗の
による変換結果が
の偶数次の項のみで表されること」
整数 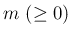 に対して、
に対して、
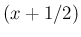 の偶数乗の
の偶数乗の 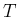 の変換結果は
の変換結果は 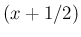 の
奇数次の項のみの式で表されることがわかる。
同様に、
の
奇数次の項のみの式で表されることがわかる。
同様に、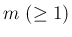 に対して、
に対して、
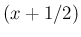 の奇数乗の
の奇数乗の 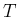 の変換結果は
の変換結果は 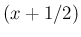 の
偶数次の項のみの式で表される。
これで [S1],[S2] が成り立つことが示され、
よって [T1],[T2] が示されたことになる。
の
偶数次の項のみの式で表される。
これで [S1],[S2] が成り立つことが示され、
よって [T1],[T2] が示されたことになる。
竹野茂治@新潟工科大学