7 μ(N,m)
6 節で求めた 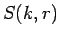 から
から 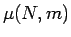 を計算してみる。
(16) を (4) に代入すると、
を計算してみる。
(16) を (4) に代入すると、
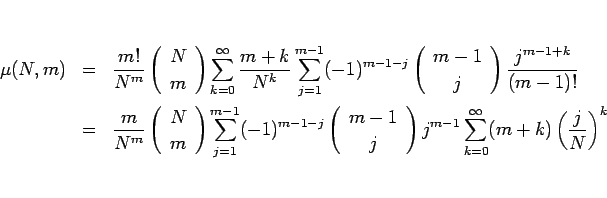
となる。
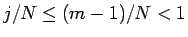 であるから、最後の和は収束し、
(1), (2) より
であるから、最後の和は収束し、
(1), (2) より
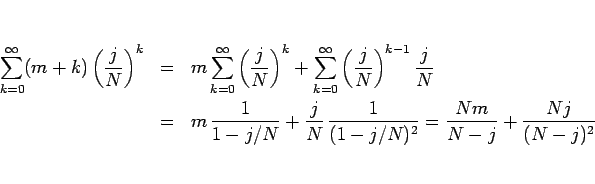
となるので、
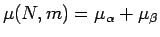 と分け、
と分け、
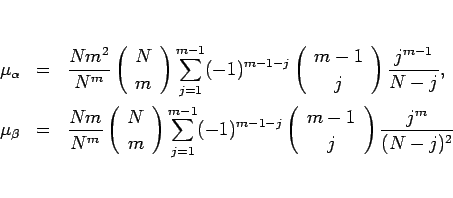
と書けることになる。
まずは 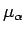 の和の部分を考える。
の和の部分を考える。
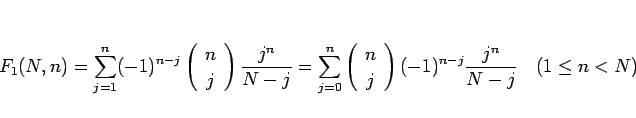
とし 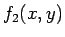 を、
を、
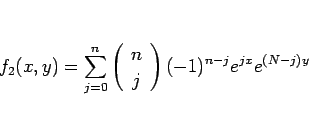
とすると、二項定理より
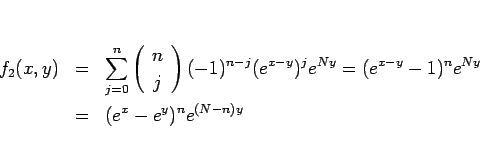
となる。一方、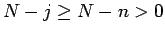 なので、
なので、
![\begin{displaymath}
\int_{-\infty}^0 e^{(N-j)y} dy
=\left[\frac{1}{N-j}e^{(N-j)y}\right]_{y=-\infty}^{y=0}
=\frac{1}{N-j}
\end{displaymath}](img144.gif)
が成り立つから、
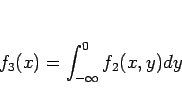
とすれば、
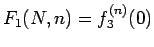 となることになる。
となることになる。
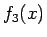 の積分を
の積分を 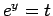 と置換して計算すると、
と置換して計算すると、
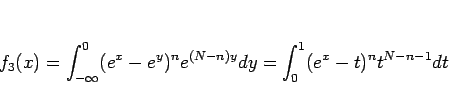
となるが、これをさらに 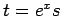 と置換すると、
と置換すると、
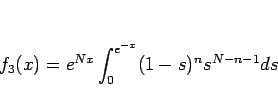
となる。この積分の部分を 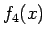 とすると、
とすると、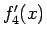 のテイラー展開は
のテイラー展開は
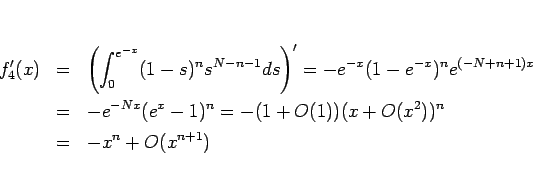
となるので、これを積分すれば
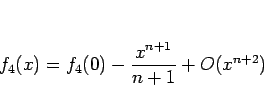 |
(17) |
であることがわかる。よって 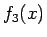 は
は
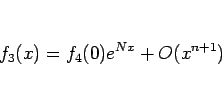
となり、よって 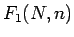 は
は
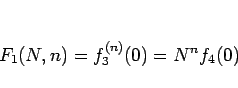
と表される。
ここで 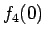 はベータ関数で書け、
はベータ関数で書け、
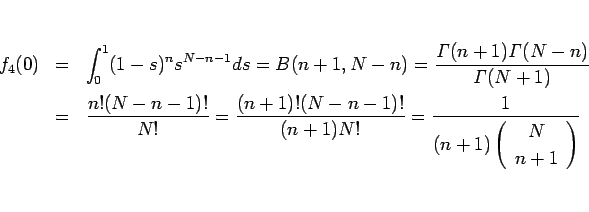
となり、結局 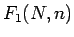 は
は
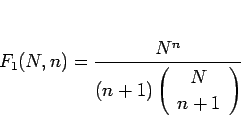
と書けることになる。これにより 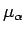 は
は
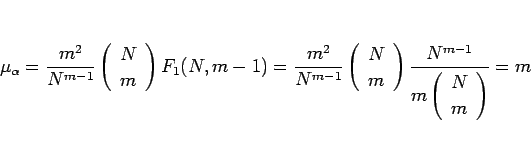 |
(18) |
となる。
次に 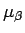 の和の部分
の和の部分
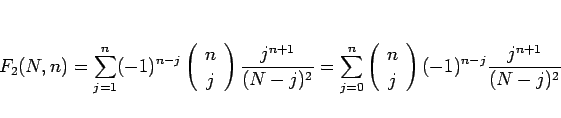
を考える (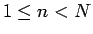 )。
この場合、
)。
この場合、
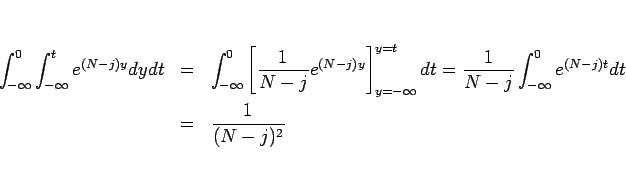
を利用して、
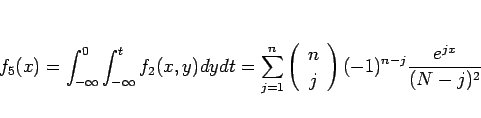
とすれば、
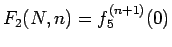 となることがわかる。
一方
となることがわかる。
一方 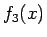 と同様の計算により
と同様の計算により 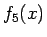 は
は
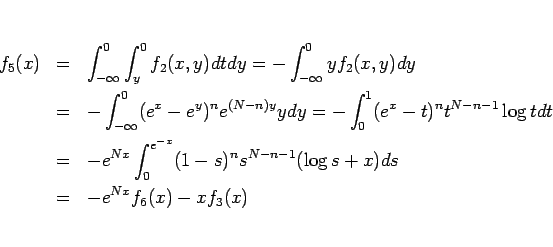
と変形できる。ここで 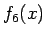 は
は
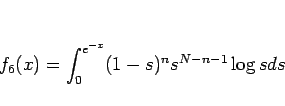
とする。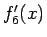 のテイラー展開は、
のテイラー展開は、
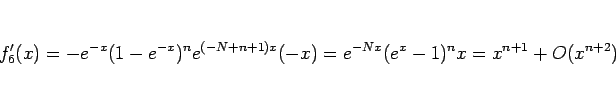
となるので、これを積分すれば
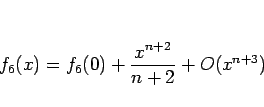 |
(19) |
となるから、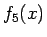 は (17), (19) より
は (17), (19) より
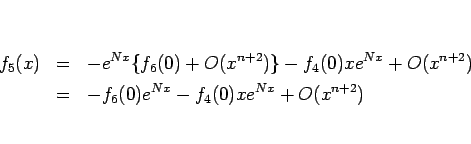
となるので、よって 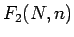 は
は
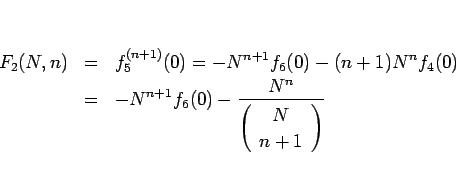
と表されることになる。よって 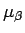 は、
は、
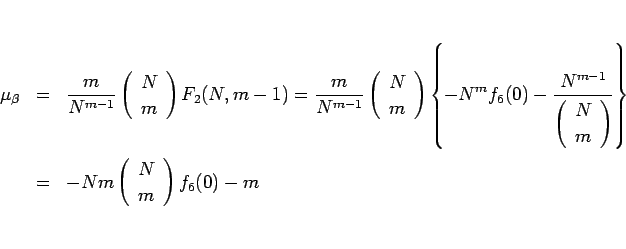
となり、(18) より、
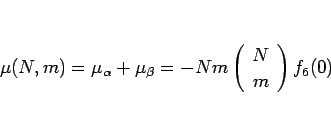 |
(20) |
となるので、結局この
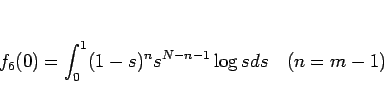
を求めればいいことになる。
竹野茂治@新潟工科大学
2008年5月24日
![]() の和の部分を考える。
の和の部分を考える。
![]() の積分を
の積分を ![]() と置換して計算すると、
と置換して計算すると、