剛体 ![]() の重心
の重心
![]() には、
には、
![]() の質量に対する重力
の質量に対する重力
![]() (
(
![]() ,
, ![]() は重力加速度) がかかり、
つなぎ目
は重力加速度) がかかり、
つなぎ目
![]() ,
,
![]() の場所では、
の場所では、
![]() ,
, ![]() からの力がかかる。
からの力がかかる。
![]() が
が
![]() の場所で
の場所で ![]() に及ぼす力
を
に及ぼす力
を
![]() とすると、その反作用により、
とすると、その反作用により、
![]() は
は
![]() の場所で
の場所で ![]() に
に
![]() の
力を及ぼすことになる。
の
力を及ぼすことになる。
よって、![]() の運動方程式は、
の運動方程式は、
次は
![]() を中心とする回転運動の方程式を考える。
を中心とする回転運動の方程式を考える。
![]() は単位ベクトル
は単位ベクトル
![]() に垂直で、
に垂直で、
![]() では
では
![]() 方向の力によって
方向の力によって
![]() が増える回転をする (3)。
が増える回転をする (3)。
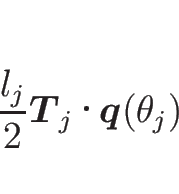
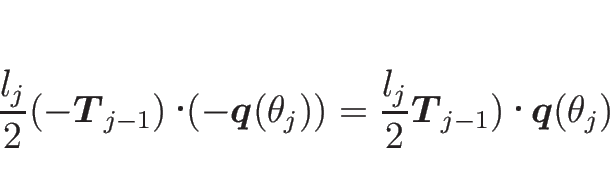
慣性モーメント ![]() は、長さ
は、長さ ![]() と線密度
と線密度 ![]() により
により
(3) の運動方程式は、2 次元ベクトルなので、
成分で考えれば ![]() 本あり、(6) は
本あり、(6) は ![]() 本あるので
合計
本あるので
合計 ![]() 本、
未知関数は
本、
未知関数は
![]() を成分で考えれば
を成分で考えれば ![]() 個、
個、
![]() が
が ![]() 個なので、
(3) と (6) から
個なので、
(3) と (6) から
![]() を消去すれば、
を消去すれば、
![]() に対する丁度
に対する丁度 ![]() 本の方程式が得られることになる。
本の方程式が得られることになる。
竹野茂治@新潟工科大学