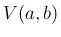
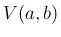 で
積分して、ほぼ (1) に対応するものを積分方程式から
改めて導いたが、
で
積分して、ほぼ (1) に対応するものを積分方程式から
改めて導いたが、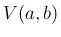 で積分して
で積分して 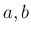 の任意性を利用して
の任意性を利用して 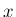 に
関する微分方程式を導くのは、(6) を導く過程から
考えれば 2 度手間になっている。
に
関する微分方程式を導くのは、(6) を導く過程から
考えれば 2 度手間になっている。
むしろ、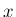 方向の積分を外して、
3 次元圧縮性オイラー方程式 (6) を
方向の積分を外して、
3 次元圧縮性オイラー方程式 (6) を 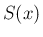 上で
上で
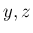 にのみ微分するだけで 3 節と同じものが
得られるはずである。本節ではそれを紹介する。
にのみ微分するだけで 3 節と同じものが
得られるはずである。本節ではそれを紹介する。
ただし、3 節では、3 次元体積分に対する
発散定理や境界条件のおかげで断面 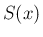 や
壁
や
壁 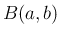 などの数式表示、パラメーター表示は必要なかったが、
などの数式表示、パラメーター表示は必要なかったが、
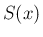 上での積分の場合、Green の公式は使えるものの、
発散定理が使えず、少し議論が難しくなるものがあり、
また、
上での積分の場合、Green の公式は使えるものの、
発散定理が使えず、少し議論が難しくなるものがあり、
また、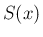 の境界積分 (線積分) が出てくるので、
境界のパラメータ表示も必要になる。
の境界積分 (線積分) が出てくるので、
境界のパラメータ表示も必要になる。
壁 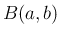 は、各断面
は、各断面 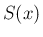 の境界線
の境界線 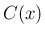 の
の
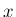 毎のパラメータ表示を使って、以下のように表されているとする。
毎のパラメータ表示を使って、以下のように表されているとする。
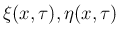 は連続かつ区分的に
は連続かつ区分的に 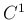 な関数で、
な関数で、
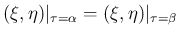
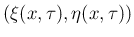 は
は 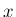 を
固定すれば
を
固定すれば 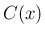 のパラメータ表示になっていて、
かつそれは
のパラメータ表示になっていて、
かつそれは 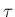 の増加に沿って
の増加に沿って 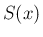 を左側に見ながら
反時計回りに進むものとする。
を左側に見ながら
反時計回りに進むものとする。
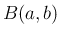 のパラメータ表示 (13) の
最も典型的なものは、極形式
のパラメータ表示 (13) の
最も典型的なものは、極形式
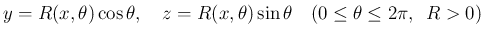
この場合、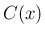 の接線ベクトル
の接線ベクトル
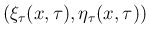 は
は
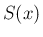 が左に接するので、それを
が左に接するので、それを 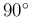 時計回りに回転したベクトル
時計回りに回転したベクトル
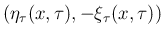 は
は 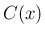 の、
の、
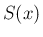 に対して外向きの法線ベクトルとなる。
に対して外向きの法線ベクトルとなる。
(13) より、
となる。 ここで、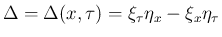 とした。
これは、
とした。
これは、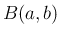 の法線ベクトルで、
の法線ベクトルで、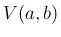 に関して外向きになる。
よって、
に関して外向きになる。
よって、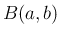 の外向き単位法線ベクトル
の外向き単位法線ベクトル
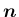 は
となる。
よって、境界条件 (7) は、
となる。
は
となる。
よって、境界条件 (7) は、
となる。
本節でも、
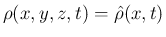 等
は 3 節と同じとし、
まず、(6) の 1 本目を
等
は 3 節と同じとし、
まず、(6) の 1 本目を 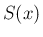 で積分する。
で積分する。
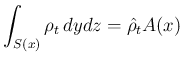
 ,
,  方向の微分は Green の公式より、
方向の微分は Green の公式より、
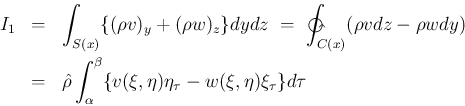
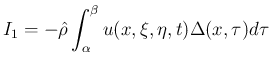
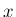 方向の微分に対しては、
5 節の補題 1 を用いる。
方向の微分に対しては、
5 節の補題 1 を用いる。
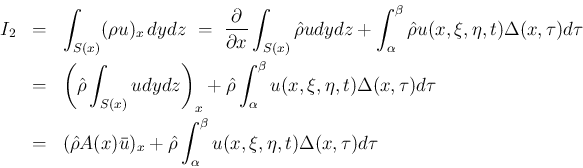
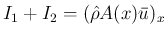
次は、(6) の 2 本目の 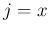 の式を
の式を 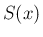 で
積分する。1 本目同様、Green の公式と補題 1 を用いる。
で
積分する。1 本目同様、Green の公式と補題 1 を用いる。
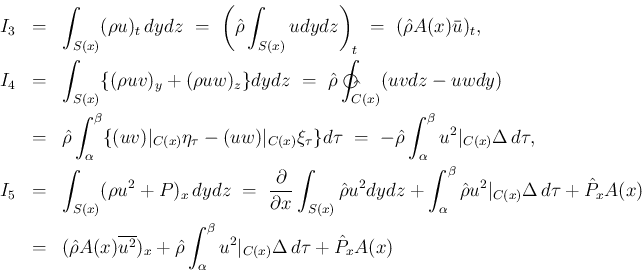
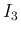 ,
, 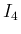 ,
, 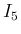 の和 (=0) により、
(9) が得られる。
の和 (=0) により、
(9) が得られる。
同じく、(6) の 2 本目の 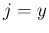 の式を
の式を 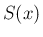 で
積分すると、
で
積分すると、
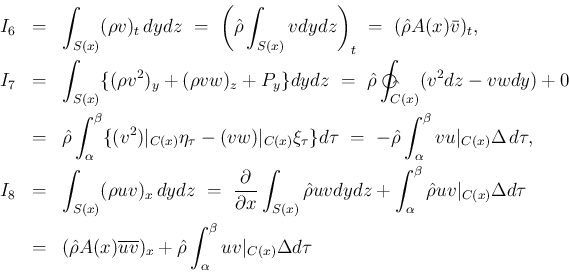
 より (10) が得られる。
同様に、
より (10) が得られる。
同様に、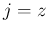 の式の積分により、(11) が得られる。
の式の積分により、(11) が得られる。
最後は (6) の 3 本目の積分。
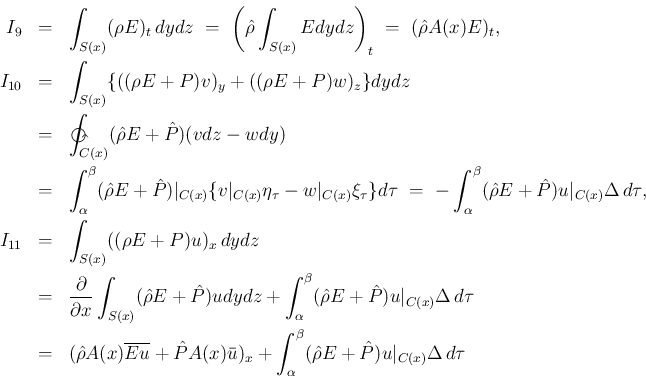
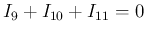 により (12) が
得られる。
により (12) が
得られる。
竹野茂治@新潟工科大学