2 概要
本稿では、以下の形の 3 乗根と
平方根の 2 重根号を外す方法について考察する。
![\begin{displaymath}
X = \sqrt[3]{a+b\sqrt{c}}
\hspace{1zw}(a,b,c\in \mathbb{Q},\ \sqrt{c}\not\in\mathbb{Q})\end{displaymath}](img1.gif) |
(1) |
ここで、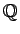 は有理数全体の集合とし、以後同様に、
は有理数全体の集合とし、以後同様に、
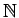 ,
, 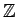 ,
, 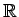 ,
, 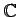 を
それぞれ自然数全体の集合、整数全体の集合、実数全体の集合、
複素数全体の集合を表すのに使用する。
を
それぞれ自然数全体の集合、整数全体の集合、実数全体の集合、
複素数全体の集合を表すのに使用する。
3 次方程式の解の公式を使うと、実は解は易しい形の解なのに、
3 乗根と平方根の 2 重根号で表されてしまう場合がある。
例えば、
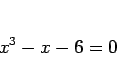 |
(2) |
という 3 次方程式の左辺は因数分解できて、
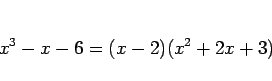 |
(3) |
となるので、(2) の解は
となる。
しかし、(2) を解の公式、
すなわち 3 次方程式の一般的な解法を用いて解くと、
この解のうち 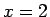 は
は
![\begin{displaymath}
x = \sqrt[3]{3+\,\frac{11}{9}\sqrt{6}} + \sqrt[3]{3-\,\frac{11}{9}\sqrt{6}}\end{displaymath}](img11.gif) |
(4) |
となり、この 3 乗根と平方根の 2 重根号を外すことが容易ではないため、
これが 2 であることはなかなかわからない。
この (2) を (3) の形に
因数分解することと、(4) の「2 重根号を外す」こと
では前者の方が易しいので、
本稿ではむしろ「2 重根号を外す」ことに 3 次方程式の因数分解を利用することを考える。
ちなみに、上の例の (4) の 2 重根号については、
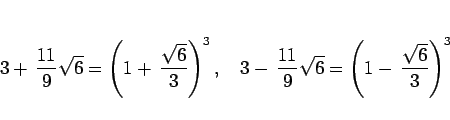 |
(5) |
が成り立つので、これにより (4) は確かに
となることがわかる。
しかし、(5) を見つけることは容易ではない。
例えば、
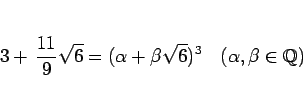 |
(6) |
と置いて、このような有理数 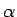 ,
, 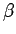 があるかどうかを考えてみると、
があるかどうかを考えてみると、
より 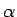 ,
, 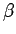 は
は
を満たすことになるが、この連立方程式を解くのは容易ではない。
また、平方根と平方根の 2 重根号の場合もそうであるが、
そもそも (6) が
成り立つのはかなり特殊な状況で、通常はむしろ
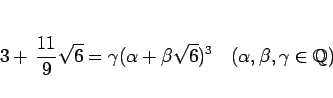 |
(7) |
の形で考える必要がある。
そのような
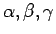 を見つけるのは相当厄介な問題で、
それがあるかどうかも容易にはわからない。
を見つけるのは相当厄介な問題で、
それがあるかどうかも容易にはわからない。
それに比べて、有理数係数の 3 次式の因数分解の方がむしろ易しく、
その方法はかなり確立されているし、
それが有理数の範囲で因数分解できるかどうかも容易に判定できる。
つまり、3 次方程式の解の公式を使って (2) の
解の 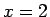 を求めることは難しいが、
因数分解により
を求めることは難しいが、
因数分解により 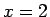 を求めることは難しくないので、
それを
を求めることは難しくないので、
それを
![$\sqrt[3]{3+11\sqrt{6}/9}$](img21.gif) の 2 重根号を外すことに利用する、
というのが本稿の目的である。
の 2 重根号を外すことに利用する、
というのが本稿の目的である。
竹野茂治@新潟工科大学
2018-03-02
![]() は
は
![]() を求めることは難しいが、
因数分解により
を求めることは難しいが、
因数分解により ![]() を求めることは難しくないので、
それを
を求めることは難しくないので、
それを
![$\sqrt[3]{3+11\sqrt{6}/9}$](img21.gif) の 2 重根号を外すことに利用する、
というのが本稿の目的である。
の 2 重根号を外すことに利用する、
というのが本稿の目的である。