3 各状態の比率の継承
次に、各状態の分布 (比率) が、どのように次の世代に継承されるか、
ということを考えてみる。
簡単のため、男女は同数であるとし、
各夫婦は 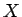 ,
, 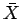 の状態にかかわらず
同程度の子を作ると考えることにする。
の状態にかかわらず
同程度の子を作ると考えることにする。
男性の 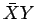 の割合を
の割合を 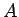 とし、
よって
とし、
よって 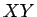 の割合を
の割合を 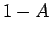 とする。
同様に、女性の
とする。
同様に、女性の
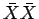 の割合を
の割合を 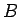 ,
,
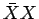 の割合を
の割合を 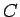 とし、
よって、
とし、
よって、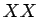 の割合を
の割合を 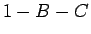 とする。
とする。
このとき、次の子の世代のそれぞれの割合を求めることにする。
子の世代の割合を、ここでは 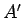 ,
, 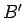 ,
, 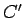 のように書くことにする。
のように書くことにする。
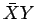 と
と
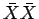 の子の場合
の子の場合
まず、このような親の組み合わせの割合は、
男女それぞれの比率が 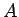 ,
,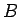 なので、
すべての夫婦に対して
なので、
すべての夫婦に対して 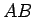 の割合で起こることに注意する。
の割合で起こることに注意する。
そして、この場合は、子には
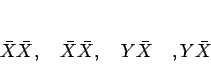
の 4 通り、つまり実質 2 通りが現れる。
つまり、子の世代での男性のうち、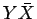 の割合
の割合 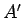 には、
この親の組合せの割合である
には、
この親の組合せの割合である 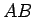 が、
女子のうち
が、
女子のうち
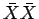 の割合
の割合 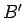 にも
にも 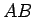 が含まれることになる。
が含まれることになる。
なお、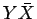 になるか
になるか
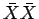 になるかは 1/2 であるから、
になるかは 1/2 であるから、
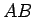 ではなく
ではなく 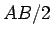 ではないかと思うかもしれないが、
ではないかと思うかもしれないが、
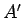 は、「男性のうちの」
は、「男性のうちの」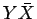 の割合であるから、
1/2 をつける必要はない。
の割合であるから、
1/2 をつける必要はない。
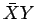 と
と 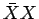 の子の場合 (夫婦の割合は
の子の場合 (夫婦の割合は 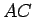 )
)
この場合は、子供は
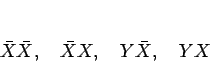
の 4 種類が同程度に起こりうる。
この夫婦の割合は 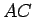 なので、
なので、
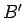 に
に 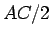 ,
, 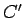 に
に 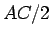 ,
, 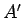 に
に 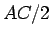 ,
, 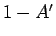 に
に 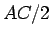 が
含まれることになる。
が
含まれることになる。
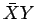 と
と 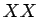 の子の場合 (夫婦の割合は
の子の場合 (夫婦の割合は 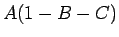 )
)
この場合は、
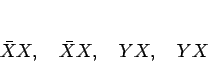
の実質 2 種類なので、
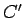 と
と 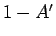 に
に 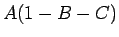 が含まれる。
が含まれる。
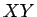 と
と
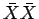 の子の場合 (夫婦の割合は
の子の場合 (夫婦の割合は 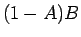 )
)
この場合は、
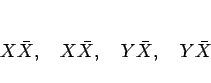
の実質 2 種類なので、
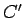 と
と 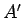 に
に 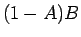 が含まれる。
が含まれる。
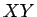 と
と 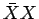 の子の場合 (夫婦の割合は
の子の場合 (夫婦の割合は 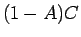 )
)
この場合は、
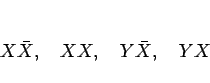
の 4 種類なので、
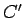 ,
, 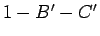 ,
, 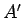 ,
, 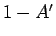 に
に 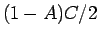 が含まれる。
が含まれる。
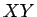 と
と 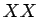 の子の場合 (夫婦の割合は
の子の場合 (夫婦の割合は 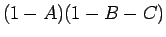 )
)
この場合は、
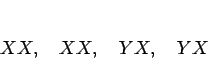
の 2 種類なので、
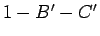 ,
, 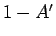 に
に 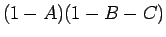 が含まれる。
が含まれる。
結局以上により、
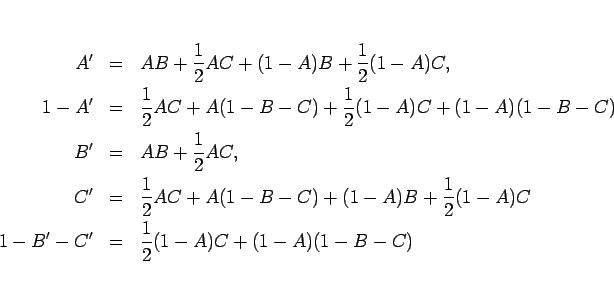
が得られることになる。それぞれ展開すると、
となる。
(1), (2) の右辺の和、
(3), (4), (5) の右辺の和が
それぞれ 1 となることは容易に確認できるだろう。
この (1)-(5) を用いれば、
親から次の世代への割合の継承が計算できることになる。
例えば、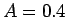 ,
, 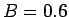 ,
, 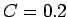 の場合、
の場合、
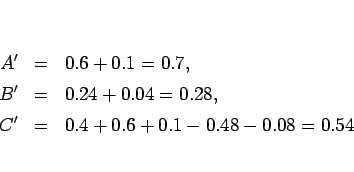
のようになる。同様に、孫の世代まで計算すれば、表 1 のようになる。
表 1:
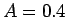 ,
, 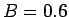 ,
, 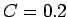 の場合
の場合
| |
男性 |
女性 |
| |
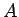 ( (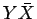 ) ) |
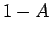 ( (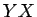 ) ) |
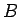 ( (
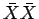 ) ) |
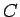 ( (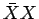 ) ) |
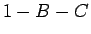 ( (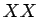 ) ) |
| 親 |
0.4 |
0.6 |
0.6 |
0.2 |
0.2 |
| 子 |
0.7 |
0.3 |
0.28 |
0.54 |
0.18 |
| 孫 |
0.55 |
0.45 |
0.385 |
0.48 |
0.135 |
|
竹野茂治@新潟工科大学
2007年9月4日
![]() ,
, ![]() の状態にかかわらず
同程度の子を作ると考えることにする。
の状態にかかわらず
同程度の子を作ると考えることにする。
![]() の割合を
の割合を ![]() とし、
よって
とし、
よって ![]() の割合を
の割合を ![]() とする。
同様に、女性の
とする。
同様に、女性の
![]() の割合を
の割合を ![]() ,
,
![]() の割合を
の割合を ![]() とし、
よって、
とし、
よって、![]() の割合を
の割合を ![]() とする。
とする。
![]() ,
, ![]() ,
, ![]() のように書くことにする。
のように書くことにする。
![]() ,
,![]() なので、
すべての夫婦に対して
なので、
すべての夫婦に対して ![]() の割合で起こることに注意する。
の割合で起こることに注意する。
![]() になるか
になるか
![]() になるかは 1/2 であるから、
になるかは 1/2 であるから、
![]() ではなく
ではなく ![]() ではないかと思うかもしれないが、
ではないかと思うかもしれないが、
![]() は、「男性のうちの」
は、「男性のうちの」![]() の割合であるから、
1/2 をつける必要はない。
の割合であるから、
1/2 をつける必要はない。
![]() ,
, ![]() ,
, ![]() の場合、
の場合、