3 パラメータの満たすべき方程式

まずは、位置の条件 [ア] を (1) に代入する。 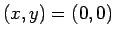$(x,y)=(0,0)$ を代入すると、

$$0 = \frac{1}{k}\cosh a + b$$

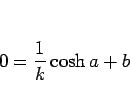
より 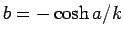$b = -\cosh a/k$ となるから、(1) は

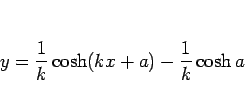$$y = \frac{1}{k}\cosh(kx+a) - \frac{1}{k}\cosh a$$ (2)

と表されることになる。 この式 (2) に 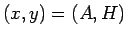$(x,y)=(A,H)$ を代入すると

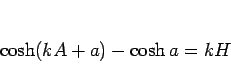$$\cosh(kA+a)-\cosh a = kH$$ (3)

が得られる。

次に条件 [イ] であるが、曲線の長さは

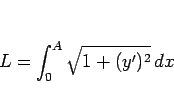$$L=\int_0^A\sqrt{1+(y')^2}\, dx$$ (4)

で得られるが、(2) より

$$\sqrt{1+(y')^2} \ =\ \sqrt{1+\sinh^2(kx+a)} \ =\ \sqrt{\cosh^2(kx+a)} \ =\ \cosh(kx+a)$$

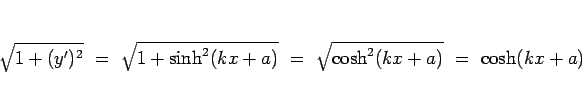
となるので (詳しくは、[1] を参照)、

$$\int_0^A\cosh(kx+a)\,dx \ =\ \left[\frac{1}{k}\sinh(kx+a)\right]_{x=0}^{x=A} \ =\ \frac{1}{k}\sinh(kA+a)-\frac{1}{k}\sinh a$$

となり、よって [イ] は、

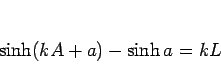$$\sinh(kA+a)-\sinh a = kL$$ (5)

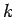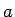となる。 この 2 つの条件 (3), (5) から 2 つのパラメータ $k$ と $a$ を決めることが目的となる。