4 グリッサンド音
グリッサンド (ポルタメントととも言う) とは、
音程を連続的に変化させる奏法のことを言う。
これは、ピアノ、クラリネット、トランペットのように
中途半端な音を出せない (出しにくい) 楽器では難しいが3、トロンボーンやバイオリンなどでは可能な、特別な奏法である。
例えば、グリッサンドでなく、
半音ずつ音階の音を 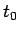 秒毎に一定に上げて行くには、
秒毎に一定に上げて行くには、
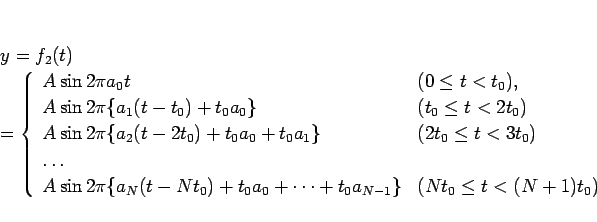 |
(3) |
のようにすればよい。
なお、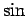 の中に
の中に 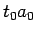 ,
, 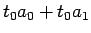 ,...のように
残してあるのは、
,...のように
残してあるのは、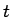 に関して連続関数にするためのものである。
に関して連続関数にするためのものである。
この (3) の 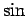 の中の
の中の 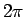 以外の部分を
以外の部分を
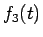 (すなわち
(すなわち
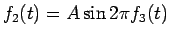 ) とすると、
この
) とすると、
この 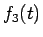 は、折れ線のグラフになる。
は、折れ線のグラフになる。
図 1:
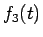 のグラフ
のグラフ
|
|
しかし、この場合は 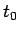 秒毎に音程が一つずつ上がっていくだけで、
連続的に音程が変化するグリッサンドにはなっていない。
連続に音程を変化させるには、この折れ線を滑らかなグラフにすればよい。
秒毎に音程が一つずつ上がっていくだけで、
連続的に音程が変化するグリッサンドにはなっていない。
連続に音程を変化させるには、この折れ線を滑らかなグラフにすればよい。
この関数 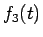 を
を 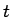 で微分すると、
微分は関数の傾きを意味するから、
そのグラフは図 2 のように階段関数となる。
で微分すると、
微分は関数の傾きを意味するから、
そのグラフは図 2 のように階段関数となる。
図 2:
導関数 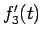 のグラフ
のグラフ
|
|
このグラフを見るとわかるが、
この導関数 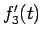 は
は 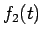 の音の周波数を表しているようである。
まずこの事実について説明しておく。
の音の周波数を表しているようである。
まずこの事実について説明しておく。
今、増加関数 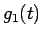 (
(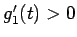 ) に対して
) に対して 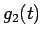 を
を
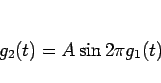 |
(4) |
とするとき、この 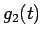 の
の 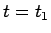 での周波数を考えてみる。
周波数とは 1 秒あたりの波の数であり、
での周波数を考えてみる。
周波数とは 1 秒あたりの波の数であり、
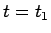 から
から
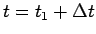 の間での波数は、
の間での波数は、
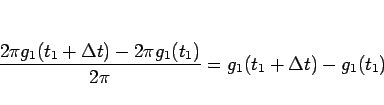
であり、よってこれを 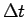 で割った
で割った
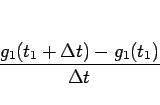 |
(5) |
が 1 秒あたりの波数、
すなわち 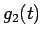 のこの
のこの 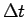 秒間の平均的な周波数となる。
この (5) の式を
秒間の平均的な周波数となる。
この (5) の式を
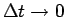 としたものが丁度
としたものが丁度 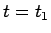 での周波数となるが、
微分の定義より、その極限は
での周波数となるが、
微分の定義より、その極限は
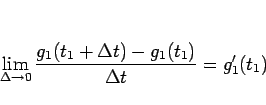
となる。つまり、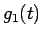 の微分係数
の微分係数 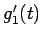 は確かに
は確かに
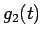 の周波数を表すことがわかる。
の周波数を表すことがわかる。
今、音程の周波数 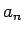 に対して、
音程と同様に一定に増加する添え字
に対して、
音程と同様に一定に増加する添え字 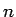 を音程を数値化したもの、
すなわち下のドを 0、ド
を音程を数値化したもの、
すなわち下のドを 0、ド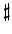 を 1 のように見ることにすれば、
を 1 のように見ることにすれば、
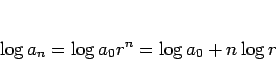
なので、
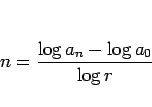
となり、この数値化された音程 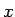 と周波数
と周波数 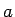 の間の関係は、
の間の関係は、
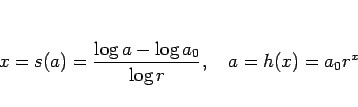 |
(6) |
と書けることになる。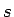 は周波数を音程に変える関数、
は周波数を音程に変える関数、
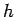 は逆に音程を周波数に変える関数となる。
は逆に音程を周波数に変える関数となる。
最初 ( ) の周波数が
) の周波数が 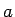 で,
で, 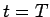 のときの周波数が
のときの周波数が 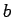 であり、
その間一定に音程が変化するような (4) の形の関数を考えてみることにする。
であり、
その間一定に音程が変化するような (4) の形の関数を考えてみることにする。
上の考察により 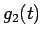 の周波数は
の周波数は 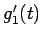 であるので、
であるので、
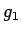 が満たすべき条件は、
が満たすべき条件は、
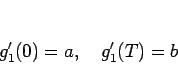 |
(7) |
および音程 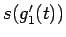 が一定に変化、すなわち直線的に変化することである。
が一定に変化、すなわち直線的に変化することである。
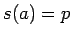 ,
, 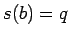 とすると、
とすると、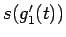 は
は 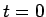 から
から 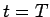 にかけて
にかけて
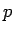 から
から 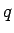 に直線的に変化することになるので、
に直線的に変化することになるので、
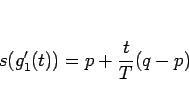
と書けることになる。よって、
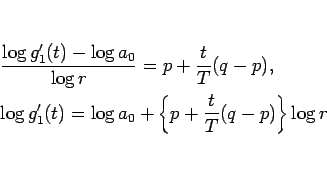
より、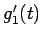 は、
は、
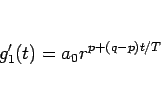 |
(8) |
となる。ここで、
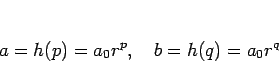
より、
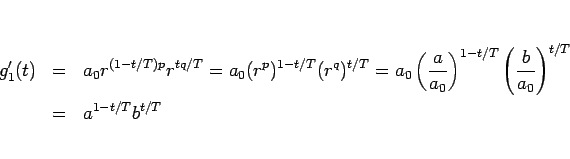
となるので、結局
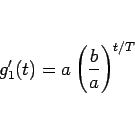 |
(9) |
と書けることになる。これを積分すれば、
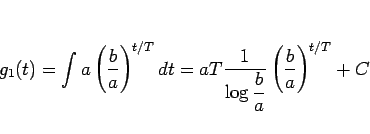
となり、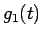 では定数差は特に意味を持たないので、
では定数差は特に意味を持たないので、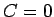 とし、
また
とし、
また 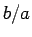 を
を 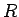 と書くことにすれば、
と書くことにすれば、
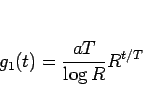 |
(10) |
と書けることになる。よって、
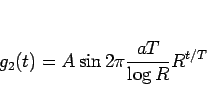 |
(11) |
が、グリッサンドを生成する関数だということになるが、
もちろん、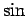 の代わりに周期が 1 の別の関数
の代わりに周期が 1 の別の関数 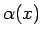 を使って、
を使って、
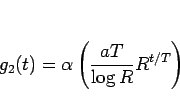 |
(12) |
としてもよい。
これは、(11) とは別の音色のグリッサンド関数となる。
竹野茂治@新潟工科大学
2007年8月7日
![]() 秒毎に一定に上げて行くには、
秒毎に一定に上げて行くには、
![]() の中の
の中の ![]() 以外の部分を
以外の部分を
![]() (すなわち
(すなわち
![]() ) とすると、
この
) とすると、
この ![]() は、折れ線のグラフになる。
は、折れ線のグラフになる。
![]() 秒毎に音程が一つずつ上がっていくだけで、
連続的に音程が変化するグリッサンドにはなっていない。
連続に音程を変化させるには、この折れ線を滑らかなグラフにすればよい。
秒毎に音程が一つずつ上がっていくだけで、
連続的に音程が変化するグリッサンドにはなっていない。
連続に音程を変化させるには、この折れ線を滑らかなグラフにすればよい。
![]() を
を ![]() で微分すると、
微分は関数の傾きを意味するから、
そのグラフは図 2 のように階段関数となる。
で微分すると、
微分は関数の傾きを意味するから、
そのグラフは図 2 のように階段関数となる。
![]() (
(![]() ) に対して
) に対して ![]() を
を
![]() に対して、
音程と同様に一定に増加する添え字
に対して、
音程と同様に一定に増加する添え字 ![]() を音程を数値化したもの、
すなわち下のドを 0、ド
を音程を数値化したもの、
すなわち下のドを 0、ド![]() を 1 のように見ることにすれば、
を 1 のように見ることにすれば、
![]() ) の周波数が
) の周波数が ![]() で,
で, ![]() のときの周波数が
のときの周波数が ![]() であり、
その間一定に音程が変化するような (4) の形の関数を考えてみることにする。
であり、
その間一定に音程が変化するような (4) の形の関数を考えてみることにする。
![]() の周波数は
の周波数は ![]() であるので、
であるので、
![]() が満たすべき条件は、
が満たすべき条件は、
![]() ,
, ![]() とすると、
とすると、![]() は
は ![]() から
から ![]() にかけて
にかけて
![]() から
から ![]() に直線的に変化することになるので、
に直線的に変化することになるので、