7 タンジェントの主値積分
さて元の問題に戻るが、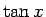 は
は 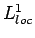 ではなく、
ではなく、
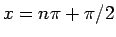 に 1 位の極があるのでこのままでは超関数とはならない。
しかし、この特異点での積分は主値積分 (principal value) を考えることで
超関数と見なすことができる。
これを本稿では
に 1 位の極があるのでこのままでは超関数とはならない。
しかし、この特異点での積分は主値積分 (principal value) を考えることで
超関数と見なすことができる。
これを本稿では
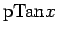 と書くことにする。
と書くことにする。
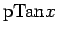 は、次のような超関数となる (
は、次のような超関数となる (
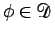 )。
)。
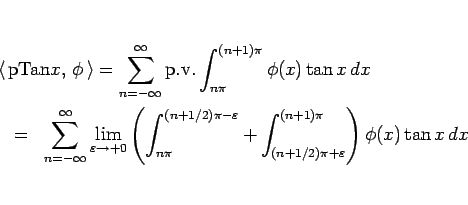
ここで、
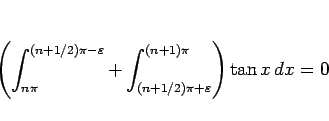
なので、
と表されることになる。
これは、
![$\mathop{\mathrm{supp}}\nolimits \phi\subset [-N\pi,N\pi]$](img182.gif) とすると (
とすると (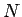 : 自然数)、
: 自然数)、
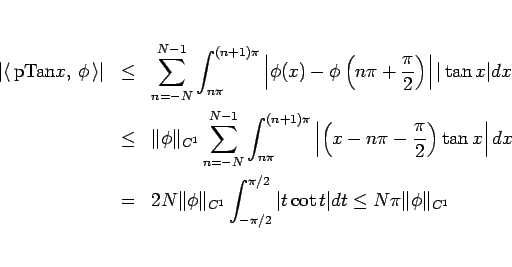
となるので、
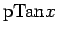 は確かに超関数となる (
は確かに超関数となる (
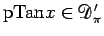 )。
)。
次に、
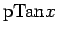 の周期積分を計算してみる。
の周期積分を計算してみる。
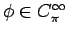 とすると、(19) と
とすると、(19) と 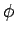 の周期性により
の周期性により
が得られる。
竹野茂治@新潟工科大学
2015年6月1日
![]() の周期積分を計算してみる。
の周期積分を計算してみる。
![]() とすると、(19) と
とすると、(19) と ![]() の周期性により
の周期性により