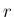 の円
の円 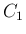 に対して、半径を
に対して、半径を 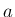 だけ増やした円
だけ増やした円 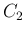 の
円周の差
の
円周の差
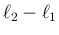 が、
が、
まず、半径 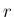 の円
の円 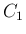 に対して、半径を
に対して、半径を 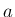 だけ増やした円
だけ増やした円 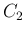 の
円周の差
の
円周の差
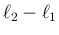 が、
が、
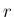 によらない値になる理由は、
円周
によらない値になる理由は、
円周 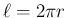 が
が 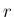 に比例するから、
より正確には
に比例するから、
より正確には 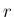 の 1 次式だからである。
の 1 次式だからである。
例えば、円周とは違い、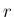 には比例しない「面積」
には比例しない「面積」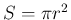 の差は、
の差は、
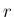 は消えず、
よって
は消えず、
よって 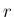 が大きくなれば
が大きくなれば 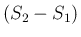 も大きくなるので
元の問題のような意外性は起きない。
も大きくなるので
元の問題のような意外性は起きない。
また、次元をあげて円の代わりに球を考えても、
球の表面積
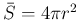 はやはり
はやはり 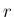 には比例しないから
表面積の差は
には比例しないから
表面積の差は
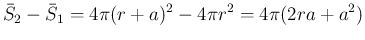
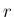 は消えない。
は消えない。
面積で無理矢理 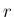 を消そうとすれば、
単純な差を考える代わりに
を消そうとすれば、
単純な差を考える代わりに
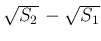 を考えれば
を考えれば 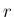 は
消えるが、それでは複雑すぎ、作為的すぎて、
やはり意外性のある問題にはならないだろう。
よって、元の問題のように結果が
は
消えるが、それでは複雑すぎ、作為的すぎて、
やはり意外性のある問題にはならないだろう。
よって、元の問題のように結果が 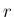 によらないという意外性は、
によらないという意外性は、
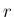 に比例する円周の場合だけに起こることになる。
に比例する円周の場合だけに起こることになる。
そして、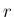 によらないことが意外性を生むもうひとつの原因は、
円であるがために (1) が
わかりにくいことだと思う。すなわち、
円周が半径に比例するために成立する式 (1) は、
図形的に言えば、
によらないことが意外性を生むもうひとつの原因は、
円であるがために (1) が
わかりにくいことだと思う。すなわち、
円周が半径に比例するために成立する式 (1) は、
図形的に言えば、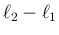 が半径
が半径 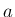 の円周 (
の円周 (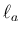 ) に一致する、
ということを意味するが (図 2)、
これが簡単には納得しづらい。
) に一致する、
ということを意味するが (図 2)、
これが簡単には納得しづらい。
逆にそれが図形的にすんなり受け入れられるのであれば、 元の問題の意外性はなくなってしまって、 面白い問題として成立しないはずである。 では、なぜ (1) が図形的に納得しづらい、 すなわち図 2 の一致がわかりにくいかと言えば、 曲率の違いに原因があるのではないかと思う。 図 2 の 3 つの円は、曲率、すなわち曲り具合が違うため、 ピッタリ重ねることができず、その長さの違いの視覚的な比較、 感覚的な理解が容易ではない。
例えば、これが円ではなく、正方形の周長の比較であれば、 重ねることが可能なので、容易に比較ができる (図 3)。
一辺が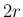 の正方形の周長
の正方形の周長
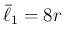 に対し、
その外側に
に対し、
その外側に  だけ広げた一辺
だけ広げた一辺 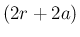 の
正方形の周長は
の
正方形の周長は
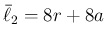 となり、その差は
となり、その差は 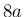 、
すなわち一辺
、
すなわち一辺 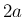 の正方形の周長となるが、
それは 図 3 のように重なる部分の引き算が視覚的に行え、
その残りの部分から小さい正方形を再構成できるため、
そうなることが感覚的に理解できる。
しかしこれと同じことは、曲率が異なる円同士では行えず、
それが感覚的な理解をさまたげているのではないかと思う。
の正方形の周長となるが、
それは 図 3 のように重なる部分の引き算が視覚的に行え、
その残りの部分から小さい正方形を再構成できるため、
そうなることが感覚的に理解できる。
しかしこれと同じことは、曲率が異なる円同士では行えず、
それが感覚的な理解をさまたげているのではないかと思う。
ただし、中心角が十分小さな扇形で考えれば (図 4)、
円弧はほぼ直線化するので、差の部分を同じ中心角の半径 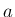 の
小さい扇形の円弧にほぼ一致すると見ることは可能であるが、
円弧は厳密には直線ではないことや、総和の際の誤差の問題、
そしてなによりこういう微分的な考察は一般向きではないことを考えると、
このような説明で感覚的に理解させるのはだいぶ無理があるように思う。
の
小さい扇形の円弧にほぼ一致すると見ることは可能であるが、
円弧は厳密には直線ではないことや、総和の際の誤差の問題、
そしてなによりこういう微分的な考察は一般向きではないことを考えると、
このような説明で感覚的に理解させるのはだいぶ無理があるように思う。
となると、元の問題の説明としては、(1) の
ような計算で示してそれで終わり、というよりも、
まず 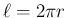 が
が  に比例すること、
および円と同様に
に比例すること、
および円と同様に  に比例する図形である正方形の周長で、
図 2 と同様のことが成立することを
図 3 で図形的に説明する方が、
むしろ納得しやすいのではないだろうか。
に比例する図形である正方形の周長で、
図 2 と同様のことが成立することを
図 3 で図形的に説明する方が、
むしろ納得しやすいのではないだろうか。
竹野茂治@新潟工科大学