4 チェビシェフの不等式の分散への適用
本節では、チェビシェフの不等式を利用して、
不偏分散と標本分散の母分散への一致性を、
不偏分散の極限を考えることに帰着させる。
まず、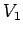 に対してチェビシェフの不等式を適用すると、
(6) より、
に対してチェビシェフの不等式を適用すると、
(6) より、
![\begin{displaymath}
P(\vert V_1-\sigma^2\vert>k)\leq\frac{1}{k^2}V[V_1]
\end{displaymath}](img54.gif)
が言えるので、よって、もし
![\begin{displaymath}
\lim_{n\rightarrow\infty}V[V_1]=0\end{displaymath}](img55.gif) |
(7) |
であれば、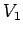 の
の 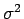 に対する一致性が言えることになる。
に対する一致性が言えることになる。
また、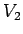 に対しては、
(6) より、チェビシェフの不等式は
に対しては、
(6) より、チェビシェフの不等式は
![\begin{displaymath}
P\left(\left\vert V_2-\frac{n-1}{n}\sigma^2\right\vert>k\right)
\leq\frac{1}{k^2}V[V_2]\end{displaymath}](img56.gif) |
(8) |
となるが、
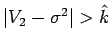 (
(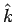 は任意の正数) のとき、
は任意の正数) のとき、
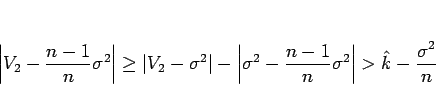
であり、また、
![\begin{displaymath}
V[V_2]
= V\left[\frac{n-1}{n}V_1\right]
= \left(\frac{n-1}{n}\right)^2V[V_1]
\end{displaymath}](img60.gif)
なので、(8) より、
![\begin{displaymath}
P(\vert V_2-\sigma^2\vert>\hat{k})
\leq P\left(\left\vert V_...
...frac{\sigma^2}{n}\right)^2}
\left(\frac{n-1}{n}\right)^2V[V_1]
\end{displaymath}](img61.gif)
となることがわかる。
よって、この場合も、(7) が言えれば、
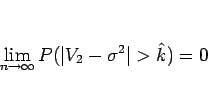
が言えることになるので、
結局 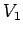 ,
, 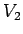 の
の 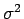 に対する一致性は、
(7) を示せばよいことになる。
に対する一致性は、
(7) を示せばよいことになる。
なお、(7) を示すために、
今後
![$E[X_i^k]=\xi_k$](img46.gif) は、
は、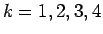 に対して「有限である」
と仮定する。
に対して「有限である」
と仮定する。
竹野茂治@新潟工科大学
2013年7月4日
![]() に対してチェビシェフの不等式を適用すると、
(6) より、
に対してチェビシェフの不等式を適用すると、
(6) より、
![]() に対しては、
(6) より、チェビシェフの不等式は
に対しては、
(6) より、チェビシェフの不等式は
![]() は、
は、![]() に対して「有限である」
と仮定する。
に対して「有限である」
と仮定する。