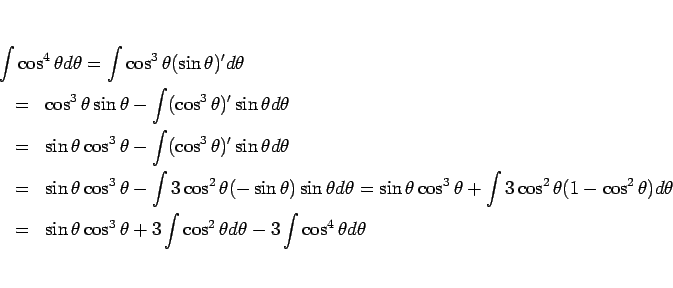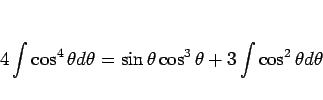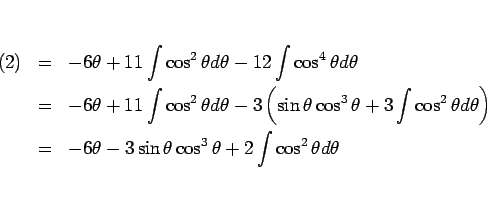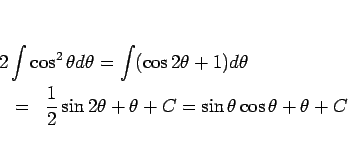次へ: 5 最後に
上へ: '有理関数の積分について (その 2)'
前へ: 3 積分の実行
(PDF ファイル: quotef2.pdf)
2 節の式を実際に計算してみよう。
前半部分の積分は、
のようになる。
後半部分は、2 通りの方法で計算してみる。
まずは、置換をしない未定係数法でやってみる。
と置き、両辺を 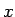 で微分する。
で微分する。
よって、
より、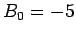 ,
, 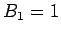 ,
, 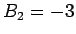 と求まり、よって
と求まり、よって
となる。
次は、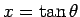 と置換してからやってみる。この場合、
と置換してからやってみる。この場合、
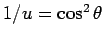 ,
,
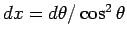 なので、
なので、
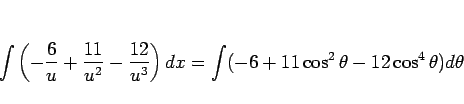 |
(2) |
であり、これは
と置ける。この式を両辺微分すると、
となるので、結局
となり、この連立方程式は置換しない場合と全く同一で、
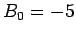 ,
, 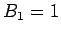 ,
, 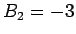 となる。よって、
となる。よって、
となる。
ついでであるから、未定係数法ではなく、
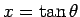 と置換したあとで部分積分による方法でも計算してみよう。
(2) から部分積分を行う。
と置換したあとで部分積分による方法でも計算してみよう。
(2) から部分積分を行う。
となるので、
となる。よって、(2) は、
となるが、倍角の公式を使えば、
となるので、結局
となり、(3) の式が得られたことになる。
次へ: 5 最後に
上へ: '有理関数の積分について (その 2)'
前へ: 3 積分の実行
竹野茂治@新潟工科大学
2006年6月2日
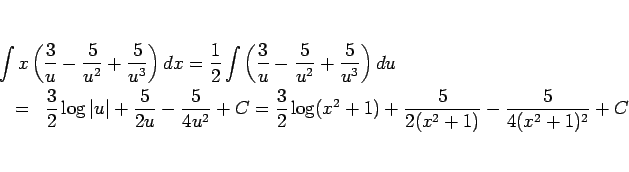
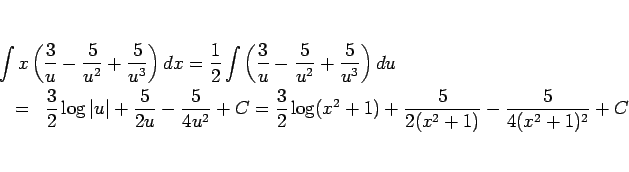
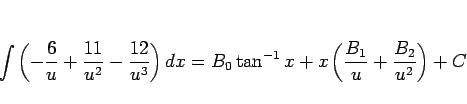
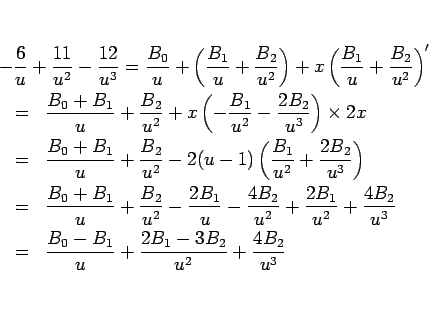
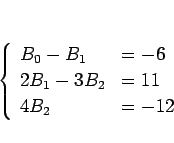
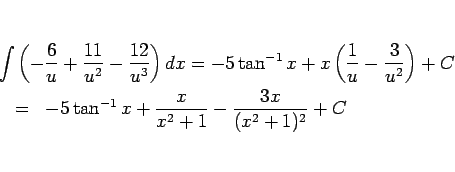
![]() と置換してからやってみる。この場合、
と置換してからやってみる。この場合、
![]() ,
,
![]() なので、
なので、
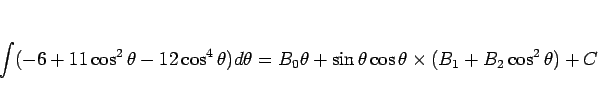
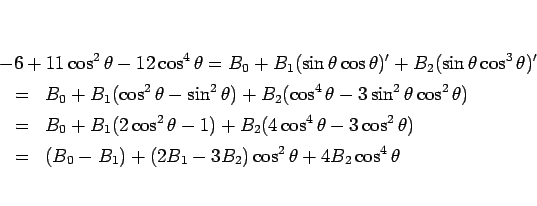
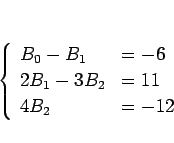
![]() と置換したあとで部分積分による方法でも計算してみよう。
(2) から部分積分を行う。
と置換したあとで部分積分による方法でも計算してみよう。
(2) から部分積分を行う。